Александр Казанский - Дискретная математика. Краткий курс. Учебное пособие

A

B = ( А \ В ) ∪ ( В \ А ).

Например, пусть А = (1, 2, 3, 4, 5, 6}, B = {4, 5, 6, 7, 8}. Тогда

А \ В = {1, 2, 3}, B \ A = {7, 8} и тогда A

B = {1, 2, 3, 7, 8}.

На рис. 1.6 на диаграмме Венна множество A

B заштриховано.

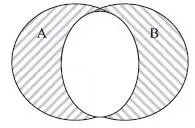
A

B заштриховано

Рис. 1.6

Операции над множествами позволяют образовывать из исходных множеств новые множества. При этом операция пересечения множеств применяется для различных практических задач, таких как классификация каких-либо объектов, анализ различного рода социологических опросов или исследований, анализ данных, из которых необходимо выбрать данные, характеризуемые заданными свойствами. Рассмотрим следующий пример. Пусть имеется список студентов группы, успешно решивших первую задачу контрольной работы (обозначим множество их фамилий как А ). Пусть также имеется список всех тех, кто успешно решил вторую задачу (множество В ), и всех тех, кто решил третью (множество С ). Если теперь потребуются сведения о тех, кто успешно решил и первую и вторую задачи одновременно, то необходимо будет выбрать тех, кто входит одновременно и в первый и во второй списки. Для этого надо найти новое множество, являющееся пересечением исходных множеств А и В , т. е. найти множество А ∩ B. Однако это множество не содержит информации о том, решили или нет данные студенты третью задачу. Ясно, что для этого потребуется найти еще одно множество, являющееся пересечением всех трех множеств, т. е. множество А ∩ В ∩ С .

Предположим теперь, что необходимо составить такой список, в котором присутствуют фамилии студентов, которые решили первую и вторую задачи, но не решили третьей. В этом случае надо найти множество А ∩ В ∩ С с.

Рассмотрение подобных случаев приводит к понятию фундаментального произведения множеств.

Пусть имеется n различных множеств А 1, А 2, А 3, …, А n. Фундаментальным произведением множествназывается множество вида

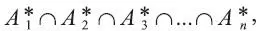
где Аi* – это либо А i , либо Аic . Заметим также, что:

1) имеется точно 2n таких фундаментальных произведений;

2) любые два таких фундаментальных произведения не пересекаются;

3) универсальное множество является объединением всех таких фундаментальных произведений.

Рассмотрим пример из трех множеств А, В и С и дадим геометрическую интерпретацию их фундаментальных произведений (рис. 1.7):

А = {1, 2, 3, 6, 7},

B = {3, 4, 5, 6},

C = {5, 6, 7, 8}.

Имеется ровно восемь фундаментальных произведений из трех множеств:

P 0 = A c ∩ B c ∩ C c = {9}

P 1 = A c ∩ B c ∩ C = {8}

P 2 = A c ∩ B ∩ C c = {4}

P 3 = A c ∩ B ∩ C = {5}

P 4 = A ∩ B c ∩ C c = {1, 2}

P 5 = A ∩ B c ∩ C = {7}

P 6 = A ∩ B ∩ C c = {3}

P 7 = A ∩ B ∩ C = {6}

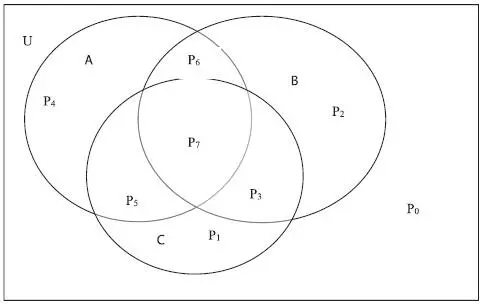
Рис. 1.7

Для данного множества S можно рассматривать множество всех его подмножеств. При этом придется рассматривать множество, элементами которого будут также множества, т. е. множество множеств. Чтобы избегать путаницы, часто бывает более удобно говорить о классе множеств или о семействе множеств. Если необходимо рассмотреть множества из данного класса, то можно говорить о подклассе или подсемействе. Например, рассмотрим множество S = { a, b, c, d }. Пусть А класс подмножеств S из трех элементов. Тогда

А = [{ a, b, c }, { a, b, d }, { a, c, d }, { d, c, d }].

Элементами класса А являются множества { a, b, c }, { a, b, d }, { a, c, d } и { b, c, d }].

Пусть теперь В класс подмножеств S , который содержит элемент а и два других элемента из S . Тогда

В = {{ a, b, c }, { a, b, d }, { a, c, d }]. Элементами В являются множества { a, b, c }, { a, b, d } и { a, c, d }]. Поэтому В является подклассом класса А.

Для данного множества S можно говорить о классе всех подмножеств S . Этот класс называют степенным множеством S и обозначают 2S. Если n ( S ) – число элементов множества S , то число элементов степенного множества n(2S) представляет собой степень 2 и равно n (2S) = 2 n(S). Например, если S = { a, b, c }, то степенное множество

2S = [ Ø ,{ a }, { b }, { c }, { a, b },{ a, c }, { b, c }, S ].

Заметим, что пустое множество Ø принадлежит к 2S, так как пустое множество является подмножеством S и само S принадлежит 2S, поэтому число элементов n(2S) = 23 = 8.

Рассмотрим теперь еще одно важное понятие, которое называется разбиением множества S . Разбиениеммножества S называется семейство { А i} непустых подмножеств S , для которых:

1) каждый элемент х из S принадлежит к одному из подмножеств А i;

2) подмножества из { А i} взаимно не пересекаются, т. е. если

А i ≠ А j, тогда А i ∩ А j = Ø .

Подмножества в разбиении иногда называют клетками или блоками. На рис. 1.8 представлена диаграмма Венна, изображающая разбиение прямоугольного множества точек S на пять клеток А 1, А 2, А 3, А 4, А 5.

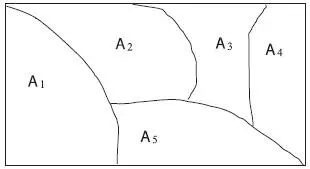
Рис. 1.8

Фундаментальные произведения также представляют собой разбиение универсального множества.

Операции объединения и пересечения могут быть распространены на любое количество множеств. Объединение состоит из таких элементов, которые принадлежат по крайней мере к одному из множеств, а пересечение из таких элементов, которые принадлежат ко всем множествам.

Абстрактная алгебра занимается изучением операций, производимых над некоторыми элементами. К настоящему времени идеи абстрактной алгебры используются не только для математических методов, но и позволяют получать практические результаты. Операции объединения, пересечения и дополнения, производимые над множествами, удовлетворят определенным законам (или тождествам) и образуют алгебру множеств. Поскольку числовая алгебра появилась раньше, то возникает вопрос, какая из операций (пересечение или объединение) «похожа» на операцию сложения чисел и какая – на операцию умножения. Ответить на этот вопрос едва ли возможно. Для чисел, например, выполняется только дистрибутивность умножения относительно сложения, а в алгебре множеств рассматривают два закона дистрибутивности: пересечения относительно объединения и объединения относительно пересечения.