Александр Казанский - Дискретная математика. Краткий курс. Учебное пособие

A: Компьютеры, которые установлены на кафедре программирования, имеют LCD-дисплеи.

B: Компьютеры университета, которые используются в учебном процессе, соединены с Интернетом.

C: Ни один компьютер кафедры программирования не соединен с Интернетом.

D: Все компьютеры, которые используются в учебном процессе, не имеют LCD-дисплеев.

Здесь утверждения А, В и С означают посылки, а утверждение D ниже линии означает заключение. Вывод правильный, если заключение D логически следует из утверждений А, В и С.

Из утверждения А компьютеры с LCD-дисплеями входят в множество компьютеров университета, а из утверждения С следует, что множество компьютеров кафедры программирования и множество компьютеров, которые соединены с Интернетом, не пересекаются.

Из утверждения В следует, что компьютеры, которые используются в учебном процессе, образуют подмножество компьютеров, которые соединены с Интернетом, как это показано на рис. 1.2.

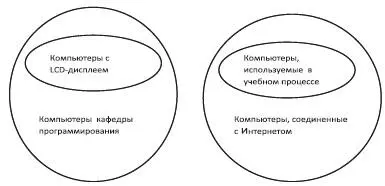
Рис. 1.2

Вывод является правильным, что видно из диаграммы Венна, поскольку множество компьютеров, используемых в учебном процессе, не пересекаются с множеством компьютеров с LCD-дисплеями.

Необходимо заметить, что, поскольку речь идет о проверке правильности вывода, истинность заключения при этом не рассматривается. Истинность заключения не является ни необходимым, ни достаточным условием правильности вывода. Если все посылки истинны, то заключение истинно. Но если хотя бы одна из посылок ложна, то заключение может быть как истинным, так и ложным, т. е. правильность вывода зависит от того, что представляют собой его посылки, и фактически определяется только его формой.

Операции над множествами позволяют получать из исходных множеств новые множества. При этом предполагается, что и сами исходные множества, и вновь полученное множество являются подмножествами одного и того же универсального множества.

Операция объединения множеств

Объединением двух множеств А и В (обозначается A ∪ B ) называется множество всех элементов, которые принадлежат к А или к В, т. е.

A ∪ B = { x: x ∈ A или x ∈ B }.

Здесь союз «или» используется в смысле и/или. На рис. 1.3 объединение A ∪ B представлено на диаграммах Венна заштрихованной областью. Если А и В непустые множества и А не совпадает с В , то возможны три различные диаграммы для объединения.

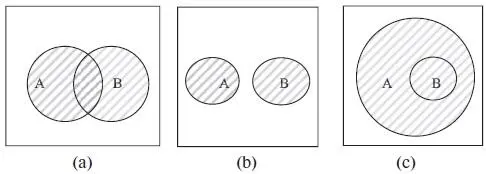
Рис. 1.3

Пример 1.4

Пусть А = {1, 2, 3, 4, 5 }, B = {1, 3, 7, 8,}, A ∪ B = = {1, 2, 3, 4, 5, 7, 9}.

Этот случай показан на рис. 1.3(а), множества имеют общие элементы {1, 3}.

Если А = {1, 2, 3, 4, 5}, B = {7, 8, 9}, то здесь множества А и В не имеют общих элементов, как показано на рис. 1.3(b), A ∪ B = {1, 2, 3, 4, 5, 7, 8, 9}.

Если А = {1, 2, 3, 4, 5, 6,}, B = {1, 2, 3}, A ∪ B = {1, 2, 3, 4, 5, 6}, то в этом случае B ⊂ A ,т. е. A ∪ B = A , как на рис. 1.3(с).

Операция пересечения множеств

Пересечением двух множеств А и В (обозначается A ∩ B ) называется множество элементов, которые принадлежат и А, и В , т. е.

A ∩ B = { x: x ∈ A и x ∈ B }.

Пересечение представлено на диаграммах Венна заштрихованной областью (рис. 1.4). Здесь, как и в случае с операцией объединения, также имеется три случая.

Если А ={1, 2, 3, 4, 5}, B = {2, 3, 6, 7, 8}, A ∩ B ={2, 3}, рис. 1.4(a).

Если A ={1, 2, 3, 4}, B ={6, 7, 8, 9 }, A ∩ B = Ø, т. е.множества А и В не пересекаются, рис. 1.4(b).

Если А ={1, 2, 3, 4, 5, 6}, B ={4, 5, 6}, A ∩ B = B = {4, 5, 6}, рис. 1.4(с).

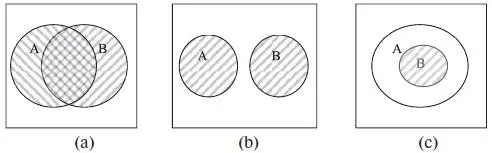
Рис. 1.4

Теорема 1.1. Следующие соотношения эквивалентны:

A ⊂ B, A ∩ B = A , и A ∪ B = B .

Следует заметить, что вопрос о том, является ли А собственным или несобственным подмножеством В , в общем, не существен, и поэтому можно записать теорему следующим образом:

A ⊆ B, A ∩ B = A , и A ∪ B = B .

Операция дополнения множеств

Если все множества рассматриваются в некоторое определенное время и являются подмножествами фиксированного универсального множества U , тогда можно определить универсальное дополнение, или просто дополнение множества А , обозначается А с, как множество элементов, которые принадлежат U , но не принадлежат А , т. е.

A с ={ x: x ∈ U, x ∉ A }.

В некоторых текстах дополнение A обозначается как A ’ или Ᾱ . На рис. 1.5(а) дополнение А с показано заштрихованной областью.

Операция разности множеств

Если подобным же образом рассматривать дополнение множества В до другого множества А , то можно получить операцию разности множеств А и В , обозначаемую как А\В , которая задает множество элементов, принадлежащих А , но не принадлежащих В , т. е.

А\В = { x: x ∈ A, x ∉ B }.

Иногда множество А \ В читается как « А минус В » и обозначается А – В . На рис. 1.5(b) разность А\В заштрихована.

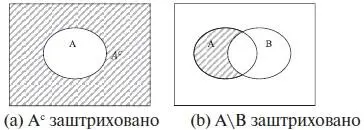
Рис. 1.5

Нетрудно заметить, что для любых двух множеств А и В выполняется тождество А\В = А ∩ В с.

Пример 1.5

Пусть универсальное множество U = N = {1, 2, 3, 4,…} является множеством натуральных чисел и пусть

А = {1, 2, 3, 4, 5}, B = {4, 5, 6, 7, 8}, C = {7, 8, 9},

и пусть D = {1, 3, 5, 7, 9,…}, множество нечетных чисел. Тогда дополнения

А с = {6, 7, 8, 9,…}, B c = {1, 2, 3, 9, 10, 11,…}, C c = {1, 2, 3, 4, 5, 6, 10, 11,…},

и разности множеств

А\В = {1, 2, 3}, А\C = {1, 2, 3, 4, 5}, B\C = {4, 5, 6}, C\B = {9},

B\A = {6, 7, 8}, A\D = {2, 4}, D c = {2, 4, 6, 8, 10,…}, множество четных чисел.

Симметрическая разность множеств

Симметрической разностью множеств А и В (обозначается A

B ) называется множество, которое состоит из элементов либо А , либо B , но не входящих в оба эти множества одновременно. Иначе говоря, это объединение этих множеств, из которого удалено их пересечение:

A

B = ( A ∪ B )\( A ∩ B ).

Можно также показать, что