Александр Казанский - Дискретная математика. Краткий курс. Учебное пособие

( A ∩ C )\( A ∩ B ∩ C ) = A ∩ В С ∩ C .

При переходе от одного шага к другому будем указывать (в правой части соответствующей строки) причины, позволяющие делать такие переходы:

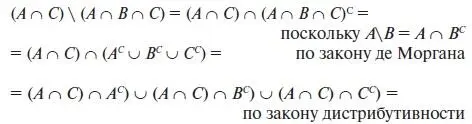
В этом примере левое выражение преобразовано в правое. Это преобразование облегчается тем обстоятельством, что известно, какое выражение должно быть получено. В то же время можно и правое выражение привести к левому. Чтобы понять, как это сделать, достаточно просмотреть первое преобразование от конца к началу. Какой путь легче, не всегда бывает сразу ясно, поэтому иногда необходимо попробовать оба способа, чтобы добиться правильного результата.

Имеется следующее существенное свойство множества натуральных чисел:

N = {1, 2, 3, …}, которое используется при построении различных доказательств.

Принцип математической индукции

Пусть Р – некоторое утверждение, определенное на положительных целых N , т. е. утверждение Р ( n ) либо истинно, либо ложно для каждого n из N . Если для Р выполняются два следующих свойства:

1) P (1) истинно;

2) P ( n +1) истинно, если истинно P ( n ), тогда Р истинно для каждого положительного целого.

Обычно этот принцип используется как аксиома для доказательства других результатов. Используем его для доказательства следующего результата.

Путь Р будет утверждением, что сумма первых n натуральных чисел, возведенных в куб, равна

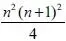
, т. е.

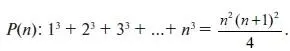
Легко видеть, что P ( n ) истинно при n = 1, т. е. P (1): 13 =

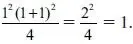
Допустим теперь, что P ( n ) истинно и докажем, что P ( n +1) также будет истинно. Для этого прибавим к обеим частям выражения для P ( n ) следующее слагаемое ( n +1)3:

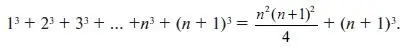
Преобразуем далее правую часть

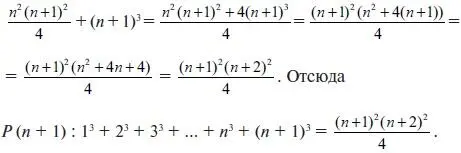
Таким образом, P ( n +1) истинно, когда истинно P ( n ). Теперь по принципу математической индукции утверждение Р истинно для всех n . Иногда принцип математической индукции записывают в более удобном для использования виде

1) P (1) истинно.

2) P ( n + 1) истинно, если истинно P ( k ) для всех 1 ≤ k < n .

Тогда Р истинно для каждого положительного целого.

При построении дискретной модели часто необходимо разбивать множества на некоторые его части, чтобы исследовать те или иные свойства исходной модели. Подобные задачи возникают как при разработке телекоммуникационных технологий, так и в различных бизнес-приложениях. Рассмотрим такой пример. Пусть элементами множества являются зоны торгового зала большого супермаркета и необходимо разбить это множество на подмножества так, чтобы каждое подмножество представляло собой совокупность зон просматриваемых одной видеокамерой, при условии, что видеокамер должно быть как можно меньше. Если зоны выбраны так, что они покрывают все помещение зала, то при этом выбранные подмножества не должны накладываться друг на друга, поскольку это приведет к неоптимальному использованию видеокамер. Кроме того, возможно, что требуется просматривать не всю площадь зала, а только некоторые ее части. Во всех таких случаях приходится рассматривать некоторое множество, представляющее собой определенную совокупность подмножеств заданного множества.

Для универсального множества U всегда можно построить его разбиение, из множеств которого легко получать требуемые совокупности. Наиболее конструктивным разбиением для этих целей является система множеств, порождаемая фундаментальными произведениями. Из 1.7 следует, что для любых n множеств можно построить разбиение S универсального множества U на 2n подмножеств, называемых фундаментальными произведениями.

Определение

Любое множество или совокупность множеств разбиения S можно представит как объединение пересечений, каждое из которых является фундаментальным произведением. Обратно, каждое непустое выражение из объединения фундаментальных произведений задает некоторое множество или совокупность множеств разбиения и такое задание однозначно определяет это множество.

Если рассматривать операцию объединения как сложение, а операцию пересечения как умножение, то подобные выражения часто называют многочленами. Эти многочлены можно преобразовывать, используя алгебраические методы. Многочлен, образованный из фундаментальных произведений, единственным образом задает любое подмножество разбиения. Будем называть такой многочлен каноническим. Осуществляя эквивалентные преобразования выражения для многочлена в каноническом виде, при котором сохраняется множество, которое он определяет, можно получать более простые выражения для аналитического задания данного множества. Если многочлен для заданного множества не допускает дальнейшего упрощения, то такой многочлен называется минимальным.

Рассмотрим пример использования многочленов.

Пример 1.6

Предположим, что в некотором университете проведена выборочная проверка посещаемости занятий девяти студентов по трем предметам: математике, информатике и английскому языку. Обозначим через А множество тех студентов, которые имеют по крайней мере один пропуск по математике. Тогда А С будет представлять собой множество студентов, которые не имеют ни одного пропуска по математике. Пусть В – множество студентов, которые имеют по крайней мере один пропуск по информатике, и С – по крайней мере один пропуск по английскому языку.

В деканат поступили следующие сведения:

– список студентов, которые не имеют пропусков занятий ни по одному из предметов, A С ∩ B С ∩ C С = Ø ;

– список студентов, которые не имеют пропусков ни по математике, ни по информатике, но имеют по английскому языку (в списке вместо фамилий будем для простоты указывать номера студентов), A С ∩ B С ∩ C = {9};