Александр Казанский - Дискретная математика. Краткий курс. Учебное пособие

Множество D также правильно определено, но его элементами являются множества, т. е. это множество множеств.

1.2. Найти список элементов для каждого из множеств:

(а) А = { x: x ∈ N, x – нечетно и x < 10},

(b) B = { x: x ∈ N ,

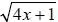
∈ N и x < 50},

(c) C = { x: x ∈ N и

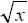
< 3 x }.

(a) А состоит из нечетных натуральных чисел, меньших 10, поэтому

A = {1, 3, 5, 7, 9};

(b) B состоит из натуральных чисел, меньших 50, для которых квадратный корень из выражения 4 х + 1 является натуральным числом, поэтому

В = {2, 6, 12, 20, 30, 42};

(с) C состоит из натуральных чисел, для которых квадратный корень меньше кубического корня из утроенного х. Это выполняется для первых 8 натуральных чисел, поэтому

С = {1, 2, 3, 4, 5, 6, 7, 8 }.

1.3. Имеются следующие множества:

А = {1, 2}, B = { 1, 3, 5 }, C = {1, 2, 7, 9 }, D = {{1}, {2}}.

Определить, корректно ли поставлены символы ∈ и ⊆

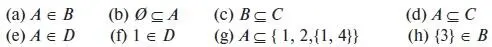
(a) A ∉ C , потому что элементами множества C не являются множества.

(b) Ø ⊆ A, потому что Ø является подмножеством каждого множества.

(c) В ⊄ С, потому что элемент 4 ∈ В , но 4 ∉ С .

(d) A ⊆ С, потому что все элементы А также принадлежат и С .

(e) А ∉ D, потому что D не имеет элемента {1, 2}.

(f) 1 ∉ D, потому что элементом множества D является не число 1, а множество {1}.

(g) A ⊆ {1, 2,{1, 4}}, поскольку все элементы А являются элементами {1, 2,{1, 4}}

(h) {3} ∉ B, потому что 3 является элементом В, а {3} – нет.

1.4. Показать, что A = {2, 3, 4, 5} не является подмножеством В = { x: x ∈ N и х – простое число}.

Для доказательства необходимо показать, что в А есть по крайней мере один элемент, которого нет в В . Рассмотрим элемент 4 ∈ А , и поскольку 4 разлагается на произведение 4 = 2 * 2, то оно не является простым и поэтому не принадлежит множеству В .

1.5. Показать, что множество А = { a, d, c, d } является собственным подмножеством B = { a, b, c, d, f, g }.

Поскольку каждый элемент А принадлежит В , то А ⊆ В . Но в В есть элемент f ∉ A , поэтому А ≠ В и, следовательно, А является собственным подмножеством В , т. е. А ⊂ В .

1.6. Для множества А = {4, 6, 8, 10} найти его несобственное подмножество.

Несобственное подмножество А должно состоять из тех же самых элементов, что и само множество А , т. е. это множество {4, 6, 8, 10}.

Операции над множествами

1.7. Найти все пересечения и объединения следующих множеств:

A = (1, 2, 3, 4, 6}, B = {3, 4, 5, 7 }, C = {6, 7, 8}.

Пересечение множеств А и В состоит только из тех элементов, которые входят и в А и в В , а объединение – из тех элементов, которые входят в А , входят в В , а также тех, которые являются общими для них, т. е. входят в их пересечение:

А ∩ В = {3, 4} А ∩ C = {6} B ∩ C = {7} А ∩ В ∩ C = Ø,

A ∪ B = {1, 2, 3, 4, 5, 6, 7} A ∪ C = {1, 2, 3, 4, 6, 8} B ∪ C ={3, 4, 7, 8},

A ∪ B ∪ C = {1, 2, 3, 4, 5, 6, 7, 8}.

1.8. Даны пересечения и объединения множеств А, В и С .

А ∩ В = {4} А ∩ C = {5} B ∩ C = {7}

A ∪ B = {1, 2, 3, 4, 5, 6, 7} A ∪ C = {1, 2, 3, 4, 5, 7, 8, 9} B ∪ C = {4, 5, 6, 7, 8, 9}.

Найти множества A, B, C .

Нетрудно видеть, что А ∩ В ∩ C = Ø , потому что нет ни одного элемента, общего для всех трех пересечений А ∩ В, А ∩ C и B ∩ C . Найдем элементы множества А . Ясно, что А содержит элементы 4 и 5, поскольку они входят в пересечение А с В и А с C . Рассмотрим пересечение множеств A ∪ B и A ∪ C , оно состоит из элементов {1, 2, 3, 4, 5, 7} и включает в себя все элементы множества А и все элементы пересечения B ∩ C = {7}. Убрав элемент 7, мы и получим множество А = {1, 2, 3, 4, 5}.

Такое же рассуждение позволяет найти и множество В . Сначала найдем пересечение двух объединений A ∪ B и B ∪ C . Это будет множество {4, 5, 6, 7}. Затем удалим из него пересечение А ∩ C = {5}, которое не входит в В , и получим множество B ={4, 5, 6}.

Чтобы найти элементы С , найдем пересечение A ∪ C и B ∪ C , которое состоит из элементов {4, 5, 7, 8, 9}, и удалим из него пересечение А ∩ В = { 4}. Элемент 4 не может входить в С , поскольку он входит и в А , и в В . Если бы он входил и в С , то тогда пересечение А ∩ В ∩ C состояло бы из элемента 4, но оно пусто. Поэтому C = {5, 7, 8, 9}.

Найти множества А, В, С можно и при помощи других рассуждений. Например, найдем множество А . Для этого удалим из множества A ∪ B все элементы множества B ∪ C и получим множество {1, 2, 3}. Оно состоит из элементов множества А и не содержит тех элементов А , которые входят в пересечение А с В и А с С . Добавив эти элементы, мы и получим множество А = {1, 2, 3, 4, 5}.

1.9. Дано универсальное множество U = {1, 2, 3, 4, 5, 6, 7, 8, 9} и множества

A = { 1, 2, 3, 4} B = {3, 4, 5, 6, 7} C = {4, 6, 7, 8, 9}.

Найти:

(a) А С, В С, С С;

(b) A\B, B\A, A\C, B\C ;

(c) A

B, A

C, B

C ;

(d) A ∪ ( B ∩ C );

(e) ( A ∩ B )C;

(f) ( A ∪ B ) ∩ ( B ∩ C )C;

(g) A С ∩ B C ∩ C .

Вспомним, что:

дополнение А С состоит из тех элементов универсального множества, которые не входят в А ;

разность множеств А\В состоит из тех элементов А , которые не принадлежат В ;

симметрическая разность A

B состоит из тех элементов А или В , которые не входят в пересечение А и В .

(a) А С = {5, 6, 7, 8, 9}; B C = {1, 2, 8, 9}; C C = {1, 2, 3, 5};

(b) A\B = {1, 2}; B\A = {5, 6, 7}; A\C = {1, 2, 3}; B\C = {3, 5};

(c) A

B = {1, 2, 5, 6, 7}; A

C = {1, 2, 6, 7, 8, 9}; B

C = = {3, 5, 8, 9};

(d) A ∪ ( B ∩ C ) = {1, 2, 3, 4, 6, 7};

(e) ( A ∩ B )C = {1, 2, 5, 6, 7, 8, 9};

(f) ( A ∪ B ) ∩ ( B ∩ C )C = {1, 2, 3, 5};

(g) A C ∩ B C ∩ C = {8, 9}.