Александр Казанский - Дискретная математика. Краткий курс. Учебное пособие

23 – 4–8 – 6 = 5 имеют только «рено»;

26 – 4–6 – 6 = 10 имеют только «ягуары»;

30 – 8–6 – 6 = 10 имеют только «понтиаки».

Заполним диаграмму на рис. 1.27.

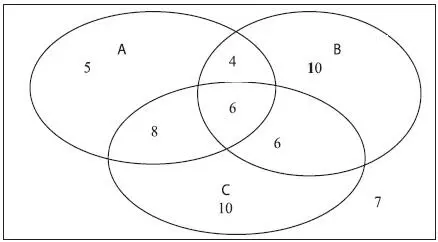
Рис. 1.27

Только одну марку автомобиля имеют 5 + 10 + 10 = 25 терминалов, что и видно из диаграммы на рис. 1.24.

Алгебра множеств и двойственность

1.16. Написать двойственное для каждого из выражений, представленных ниже:

(a) A = ( A ∩ B C) ∪ ( A ∩ B ),

(b) B = ( B ∩ U ) ∪ ( A ∩ B ),

(c) А С ∩ ( A С ∪ U )С = Ø ,

(d) ( A C ∪ B C) ∪ ( A ∩ B ) = U ,

(e) A ∩ B C ∩ C = ( A ∩ C ) ∩ ( A C ∪ B C ∪ C C).

Заменим все ∩, ∪, Ø и U в каждом равенстве и получим двойственные равенства:

(a) A = ( A ∪ B C) ∩ ( A ∪ B ),

(b) B = ( B ∪ Ø ) ∩ ( A ∪ B ),

(c) А С ∪ ( A С ∩ U )С = U,

(d) ( A C ∩ B C) ∩ ( A ∪ B ) = Ø,

(e) A ∪ B C ∪ C = ( A ∪ C ) ∪ ( A C ∩ B C ∩ C C).

1.17. Пусть имеются множества А, В, С и пусть универсальное множество U = A ∪ B ∪ C . Доказать следующие равенства:

(a) A ∩ B ∩ C С = ( A ∩ В )\( A ∩ B ∩ C ),

(b) A ∩ B C ∩ C = ( A ∩ C )\( A ∩ B ∩ C ),

(c) A C ∩ B ∩ C = ( B ∩ C )\( A ∩ B ∩ C ),

(d) A C ∩ B C ∩ C С = Ø ,

(e) A С ∩ B С ∩ C = A С ∩ В С,

(f) A C ∩ B ∩ C С = A С ∩ С С,

(g) A ∩ B C ∩ C С = B С ∩ С С,

(h) A ∩ B ∩ C = ( A ∩ В )\( А ∩ В ∩ С С).

(a) Преобразуем правую часть равенства

( A ∩ В )\( A ∩ B ∩ C ) = ( A ∩ В ) ∩ ( A C ∪ B C ∪ C C) = тождество упражнения 1.13.

= ( A ∩ В ) ∩ ( A C ∪ B C ∪ C C) =

= ( A ∩ B ∩ А C) ∪ ( A ∩ B ∩ В С) ∪ ( A ∩ B ∩ C C) = дистрибутивность

= Ø ∪ Ø ∪ ( A ∩ B ∩ C C) = по закону дополнения

= A ∩ B ∩ C C по закону тождества.

(b) ( A ∩ C )\( A ∩ B ∩ C ) = ( A ∩ C ) ∩ ( A C ∪ B C ∪ C C) =

= ( A ∩ C ∩ А C) ∪ ( A ∩ C ∩ В С) ∪ ( A ∩ C ∩ C C) =

= Ø ∪ ( A ∩ C ∩ B C) ∪ Ø = A ∩ B ∩ C C.

(c) ( B ∩ C )\( A ∩ B ∩ C ) = ( B ∩ C ) ∩ ( A C ∪ B C ∪ C C) =

= ( B ∩ C ∩ А C) ∪ ( B ∩ C ∩ В С) ∪ ( B ∩ C ∩ C C) =

= ( B ∩ C ∩ А C) ∪ Ø ∪ Ø = A C ∩ B ∩ C .

(d) A C ∩ B C ∩ C С = ( A ∪ B ∪ C )C = по закону де Моргана

= ( U )C = Ø . замена и дополнение

(e) A С ∩ В С = ( A С ∩ В С) ∩ ( С ∪ C C) = поскольку ( С ∪ C C) = U

= ( A С ∩ В С ∩ С ) ∪ ( A С ∩ В С ∩ С C) = ( A С ∩ В С ∩ С ) ∪ Ø = = ( A С ∩ В С ∩ С ).

(f) A С ∩ С С = ( A С ∩ C С) ∩ ( B ∪ B C) = поскольку ( B ∪ B C) = U

= ( A С ∩ В ∩ С C) ∪ ( A С ∩ В С ∩ С C) = ( A С ∩ В ∩ С C) ∪ Ø = = ( A С ∩ В ∩ С C).

(g) B С ∩ С С = ( B С ∩ C С) ∩ ( A ∪ A C) = поскольку ( A ∪ A C) = U

= ( A ∩ В C ∩ С C) ∪ ( A С В С ∩ С C) = ( A ∩ В C ∩ С C) ∪ Ø = = ( A ∩ В C ∩ С C).

(h) ( A ∩ В )\( А ∩ В ∩ С С) = ( A ∩ В ) ∩ ( А ∩ В ∩ С С)С = тождество упражнения 1.13.

= ( A ∩ В ) ∩ ( A С ∩ В С ∩ С ) = ( А ∩ В ∩ А C) ∪ ( А ∩ В ∩ В С) ∪ ∪ ( А ∩ В ∩ C ) =

= Ø ∪ Ø ∪ ( A ∩ B ∩ C C) = по закону тождества

= A ∩ B ∩ C .

1.18. Доказать, что для заданного универсального множества U и любого множества А ⊆ U дополнение этого множества А С единственно.

Для доказательства используем стандартный математический подход, применяемый при доказательстве единственности. Предположим, что существует два различных дополнения для А и обозначим их как А 1 c и А 2 c . Тогда каждое из них должно удовлетворять условиям дополнения

А1 c ∩ А = А 2 c ∩ А = Ø и А 1 c ∪ А = А 2 c ∪ А = U .

Поэтому

А 1 c = А 1 c ∩ U = А 1 c ∩ ( А 2 c ∪ А ) = по закону дистрибутивности

= ( А 1 c ∩ А 2 c ) ∪ ( А 1 c ∩ А ) = по закону дополнения

= ( А 1 c ∩ А 2 c ) ∪ Ø = по закону тождества

= А 1 c ∩ А 2 c .

Отсюда следует, что каждый х ∈ А 1 c является также и элементом

А 1 c ∩ А 2 c и из этого следует, что А 1 c является подмножеством А 1 c ∩ А 2 c , т. е. А 1 c ⊆ А 1 c ∩ А 2 c , но поскольку А 1 c ⊆ А 2 c по определению, то тогда А 1 c ⊆ А 2 c .

Пусть теперь

А 2 c = А 2 c ∩ U = А 2 c ∩ ( А 1 c ∪ А ) =

Выполнив преобразования, как и в первом случае, получим

= А 1 c ∩ А 2 c , т. е. А 2 c ⊆ А 1 c , но из этого следует, что

А 1 c = А 2 c = А С .

Итак, мы предположили, что существует два дополнения, а затем показали, что они совпадают, и это доказывает единственность дополнения множества А .

1.19. Известно, что для чисел операция равенства является транзитивной, т. е. если a = b и b = c , то из этого следует, что a = c . Свойство транзитивности во многих случаях оказывается очень полезным. Например, если необходимо знать, равны ли все три числа a, b и c , то достаточно проверить равенство только двух любых пар, допустим a = b и b = c , третье равенство a = c можно не проверять – оно будет выполнено в силу транзитивности. Однако если рассматривать операцию ≠, то транзитивность не выполняется. Например, a = 2, b = 3, c = 2 и тогда a ≠ b, b ≠ c , но a = c . Для множеств также операция включения множеств А ⊆ В транзитивна, но операция ⊄ не является транзитивной. Доказать, что если А ⊄ В и В ⊄ С , то из этого не следует А ⊄ С .

Для доказательства достаточно рассмотреть следующий случай. Пусть А и В непустые непересекающиеся множества, и пусть А = С . Тогда А ⊄ В и В ⊄ С , но А ⊆ С .

1.20. Для любых множеств А, В и С доказать ложность следующего утверждения: