Дмитрий Поспелов - Моделирование рассуждений. Опыт анализа мыслительных актов
- Название:Моделирование рассуждений. Опыт анализа мыслительных актов
- Автор:
- Жанр:
- Издательство:Радио и связь
- Год:1989
- Город:М.
- ISBN:5-526 00183-3
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Дмитрий Поспелов - Моделирование рассуждений. Опыт анализа мыслительных актов краткое содержание
Описываются дедуктивные, индуктивные и правдоподобные модели, учитывающие особенности человеческих рассуждений. Рассматриваются методы рассуждений, опирающиеся на знания и на особенности человеческого языка. Показано, как подобные рассуждения могут применяться для принятия решений в интеллектуальных системах.
Для широкого круга читателей.
Моделирование рассуждений. Опыт анализа мыслительных актов - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
Проверим, достигаем ли мы нужной цели с помощью данной комбинации. Если ? и ? ложны, то ложны правильные формулы (  ?&?) и (?&
?&?) и (?&  ?) и, следовательно, по свойству дизъюнкции ложна и вся большая формула. Если же ? и ? одновременно истинны, то опять обе конъюнкции ложны, так как в них входят ложные высказывания, получающиеся из истинных путем отрицания, и, следовательно, вся дизъюнкция опять является ложной. И лишь тогда, когда из двух высказываний ? и ? одно истинно, а другое ложно, мы получаем истинность всего высказывания. После этого уточнения правильная формула исчисления высказываний, соответствующая нашему примеру, примет вид (( а &((
?) и, следовательно, по свойству дизъюнкции ложна и вся большая формула. Если же ? и ? одновременно истинны, то опять обе конъюнкции ложны, так как в них входят ложные высказывания, получающиеся из истинных путем отрицания, и, следовательно, вся дизъюнкция опять является ложной. И лишь тогда, когда из двух высказываний ? и ? одно истинно, а другое ложно, мы получаем истинность всего высказывания. После этого уточнения правильная формула исчисления высказываний, соответствующая нашему примеру, примет вид (( а &((  b & c )
b & c ) 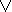 ( b &
( b &  c )))&d).
c )))&d).
Рассмотрим еще одну цитату из того же стихотворения: «…Если трон находится в стране в руках деспо?та, тогда дворянства первая забота сменить основы власти и закон». Введем два элементарных высказывания: g – «Трон находится в стране в руках деспо?та» и h – «Дворянства первая забота сменить основы власти и закон». Тогда логическая структура всего высказывания может быть представлена в виде (ЕСЛИ g ТОГДА h ). Для перехода к правильной формуле исчисления высказываний воспользуемся импликацией. Раньше она не встречалась. По определению выражение ?  ? истинно во всех случаях, кроме того, когда ? истинно, а ? ложно. Другими словами, из истинности ? в импликации, которая является истинной, всегда следует истинность ?.
? истинно во всех случаях, кроме того, когда ? истинно, а ? ложно. Другими словами, из истинности ? в импликации, которая является истинной, всегда следует истинность ?.
Исследуем запись ( g  h ). Если g истинно, то h должно быть истинно, если фраза, которая вложена Д. Самойловым в уста Пестеля, является истинной. Это хорошо, но что будет в случае, когда утверждение g ложно? Для импликации это означает, что как при истинности h , так и при его ложности вся фраза в целом остается истинной. Другими словами, если неверно, что «Трон находится в стране в руках деспо?та», то дворянство может менять основы власти и закона, а может этого и не делать. Всё равно сложное высказывание будет сохранять свою истинность. Если же мы потребуем, чтобы при ложности g всегда было бы ложным и все высказывание целиком, сохраняя остальные свойства импликации, то мы опять вернемся к конъюнкции.
h ). Если g истинно, то h должно быть истинно, если фраза, которая вложена Д. Самойловым в уста Пестеля, является истинной. Это хорошо, но что будет в случае, когда утверждение g ложно? Для импликации это означает, что как при истинности h , так и при его ложности вся фраза в целом остается истинной. Другими словами, если неверно, что «Трон находится в стране в руках деспо?та», то дворянство может менять основы власти и закона, а может этого и не делать. Всё равно сложное высказывание будет сохранять свою истинность. Если же мы потребуем, чтобы при ложности g всегда было бы ложным и все высказывание целиком, сохраняя остальные свойства импликации, то мы опять вернемся к конъюнкции.
Наверное, самым разумным с точки зрения здравого смысла было бы вообще отказаться от определения истинности или ложности выражения (ЕСЛИ ? ТОГДА ?), когда ? является ложным. Ибо для выводов в этом случае нет никакой информации. Во второй главе мы использовали знак выводимости 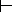 . Вот с его-то помощью и можно формализовать случай, когда в записи g
. Вот с его-то помощью и можно формализовать случай, когда в записи g 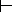 h из истинности g всегда следует истинность h , а при ложности g ничего сказать нельзя. Но знак выводимости не является логической связкой и не входит в синтаксис исчисления высказываний. Поэтому, оставаясь в рамках этого исчисления, мы вынуждены пользоваться импликацией.
h из истинности g всегда следует истинность h , а при ложности g ничего сказать нельзя. Но знак выводимости не является логической связкой и не входит в синтаксис исчисления высказываний. Поэтому, оставаясь в рамках этого исчисления, мы вынуждены пользоваться импликацией.
И еще одно замечание, касающееся импликации. Эта связка, как и разделительная дизъюнкция, может быть сведена к комбинации других связок, имеющихся в исчислении. Читатели легко могут убедиться в справедливости замены ?  ? на
? на  ?
? 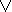 ?. Однако по ряду причин в исчислении высказываний в его классической форме импликация сохраняется как самостоятельная связка [5].
?. Однако по ряду причин в исчислении высказываний в его классической форме импликация сохраняется как самостоятельная связка [5].
Не нужно думать, что переход от фраз на естественном языке к соответствующим им правильным формулам исчисления высказываний столь прост. На этом пути стоит немало трудностей, И прежде всего потому, что частицы и союзы языка типа НЕ, И, ИЛИ, ТО, ЕСЛИ и т.п. не являются однозначными свидетельствами наличия похожих на них связок. Цитата из стихотворения «Смерть поэта» Д. Самойлова иллюстрирует это положение:
И не ведал я, было ли это
Отпеванием времени года,
Воспеваньем страны и народа
Или просто кончиной поэта.
Встречающиеся здесь И и ИЛИ не являются прямыми аналогами связок исчисления высказываний.
Мы ввели множество базовых элементов и множество синтаксических правил. Теперь необходимо ввести множество аксиом. В логике в качестве множества аксиом выбирают обычно совокупность правильных формул, которые являются общезначимыми (или тождественно истинными ). Высказывания, описываемые этими формулами, таковы, что они всегда истинны. Вот пример такого множества формул:
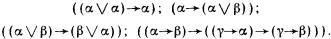
Читатели могут сами убедиться в том, что при всех комбинациях истинности и ложности формул ?, ? и ? четыре выписанные аксиомы всегда являются истинными. Такие аксиомы принято называть абсолютными или логическими .
Перейдем к описанию правил вывода R . Вспомним, что Аристотель, создавая свои силлогистические правила, добивался того, чтобы из истинных посылок всегда следовали истинные заключения. Если в качестве аксиом используются абсолютные аксиомы, то правила вывода должны обладать тем свойством, что их применение не должно нарушать истинность. Другими словами, из тождественно истинных формул должны выводиться лишь тождественно истинные формулы. Введем, учитывая это, два правила вывода исчисления высказываний.
Первое правило носит название правило подстановки . Согласно ему в формулу, которая уже выведена, можно вместо некоторого высказывания подставить любое другое при непременном условии, что эта подстановка сделана во всех местах вхождения заменяемого высказывания в данную формулу. Такая подстановка сохраняет свойство формулы быть тождественно истинной. Если в аксиому (?  (?
(? 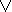 ?)) вместо ? подставить любую формулу, например (?&?), то формула ((?&?)
?)) вместо ? подставить любую формулу, например (?&?), то формула ((?&?)  ((?&?)
((?&?) 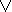 ?)) останется тождественно истинной, что легко доказывается перебором всех комбинаций истинностных значений ? и ? и проверкой того, что для всех них полученная формула остается истинной.
?)) останется тождественно истинной, что легко доказывается перебором всех комбинаций истинностных значений ? и ? и проверкой того, что для всех них полученная формула остается истинной.
Второе правило называется модус поненс (лат. modus ponens) или правило заключения и выглядит следующим образом: если ? и (?  ?) являются истинными формулами, то формула ? также истинна. Если ? является истинной, то истинность (?
?) являются истинными формулами, то формула ? также истинна. Если ? является истинной, то истинность (?  ?) означает, что ? является истинной. Поэтому правило заключения не портит истинности выводимых формул.
?) означает, что ? является истинной. Поэтому правило заключения не портит истинности выводимых формул.
Интервал:
Закладка:









