Дмитрий Поспелов - Моделирование рассуждений. Опыт анализа мыслительных актов

3. Перед всем выражением для ? 1(? 2) стоит знак отрицания, а перед ? 2(? 1) его нет. Например, ? 1= (? ?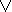), а ? 2=??.

4. Аналогичное различие, но оно касается не всего выражения для ? i ( i =1,2), а некоторого его подвыражения.

5. Скобки в ? 1расставлены не так, как в ? 2. Например, ? 1=? (? ?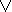), а ? 2=(? ?) ?.

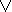6. Записи для ? 1и ? 2отличаются порядком следования подвыражений. Например, ? 1=(??) 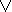?, а ? 2=? (??).

Для того чтобы иметь возможность ликвидировать подобные различия, используются 12 преобразований формул исчисления высказываний. Первые семь преобразований носят тождественный характер, т.е. не меняют истинного значения преобразуемых формул. Последние пять верны только при условии, что левая часть их является тождественно истинной ( T -выражением).

В преобразованиях использованы большие латинские буквы, которые могут соответствовать любым подвыражениям формул ? 1и ? 2. Стрелк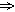и и 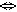показывают направление преобразований. (Знак 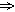есть по сути знак .)

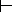С помощью этих преобразований можно устранять различия между ? 1и ? 2, которые мы перечислили выше. Укажем в специальной табл. 4 классы преобразований F 1, которые можно использовать для устранения различий. Первое различие разделено на два: различие 1 ’ требует добавления выражений в формулу, а различие 1 ’’ – вычеркивания из формулы лишних выражений.

Таблица 4

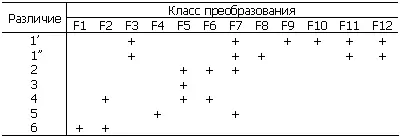
Крестики поставлены там, где можно устранить различие с помощью соответствующего преобразования.

Покажем работу программы «Логик-теоретик» на несложном примере. Пусть требуется доказать равенство ? 1=? 2, имеющее вид

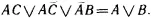
Применим к ? 1первое преобразование из F 7 справа налево. Выбор F 7 определяется различием ? 1и ? 2. Из ? 1необходимо убрать лишнее подвыражение С , которого нет в ? 2. После этого получим

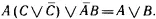
Поскольку в ? 1осталось еще выражение С , которого нет справа, то снова фиксируется различие 1 ’’ и ищется подходящее преобразование. Таким преобразованием является четвертое из F 7. Но для его применения надо сначала использовать преобразование F 1 для устранения различия 6. После этого, применяя четвертое преобразование из F 7, получаем

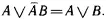
Теперь можно применить второе преобразование из F 7:

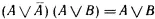
Четвертое преобразование из F 7 приводит к окончательному результату

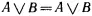
Пример, конечно, не отражает всех особенностей работы программы «Логик-теоретик». Мы несколько упростили задачу. Как видно из таблицы различий, выбор преобразования на каждом шаге далеко не однозначен. В формулах могут существовать одновременно несколько различий, а для ликвидации различия можно использовать несколько преобразований. Всякий вывод, как бы он не был организован, носит переборный характер. И успешность того или иного выбора преобразования не может быть оценена локально, в момент выбора. Поэтому программа вынуждена перебирать варианты, заходить в тупики, проходить циклы прежде, чем она сможет найти правильный путь решения. Повышение эффективности процесса вывода – центральная проблема всех автоматизированных систем дедуктивного вывода.

Исчисление высказываний не позволяет описывать дедуктивные рассуждения всех типов, в частности силлогистические умозаключения. Оно слишком бедно выразительными средствами.

Его естественным развитием является исчисление предикатов. Как и исчисление высказываний, исчисление предикатов представляет собой формальную систему. Мы не будем описывать его в такой строгой форме (любители строгости могут найти подобные описания в литературе к данному разделу), а попытаемся оставаться на содержательном уровне описания.

Под предикатом будем понимать некоторую связь, заданную на наборе из констант или переменных, например утверждение « ? больше ? ». Если семантика ? и ? не задана, то о предикате сказать особенно нечего. Пожалуй, только то, что он задает двуместное отношение, семантика которого такова, что оно является антирефлексивным (неверно, что « ? больше ? »), асимметричным и транзитивным. Но при задании семантики (т.е. областей определения переменных ? и ? ) о предикате можно будет сказать существенно больше. Если ? и ? – площади городов соответственно в СССР и Японии, то при задании списков городов и означивании переменных константами мы получим отношение между двумя высказываниями типа «Площадь Вологды больше площади Токио» или «Площадь Ленинграда больше площади Нары». После этого становится возможным говорить об истинности или ложности предиката. Для нашего примера первое означивание дает ложное значение предиката, а второе – истинное. Иногда для утверждения об истинности или ложности предиката можно обойтись и без означивания. Например, если областью определения х являются целые положительные числа, то предикат « х больше ?5» будет тождественно истинен.

В исчислении предикатов используются те же операции, что и в исчислении высказываний. С их помощью образуются предикатные формулы. Будем обозначать предикаты большими латинскими буквами. Примерами предикатных формул могут служить Р ( х , у )& Q ( a , b ) или P ( ? ) 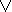P ( z , l ).

В исчислении предикатов используются два квантора: квантор общности и квантор существования . Первый обозначается как 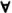, а запись 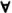xP ( x ) эквивалентна утверждению «Для всех х из области его определения имеет место Р ( х )». Второй квантор обозначается как , а запись хР ( х ) эквивалентна утверждению «Найдется по крайней мере один х * в области определения х , такой, что истинен Р ( х *)». Переменные, находящиеся в сфере действия кванторов, называются связанными , остальные переменные – свободными .