Дмитрий Поспелов - Моделирование рассуждений. Опыт анализа мыслительных актов

Вспомним И.А. Крылова: «А вы, друзья, как ни садитесь, все ж в музыканты не годитесь!». Обозначим через Р( х , у ) предикат, который связывает между собой способ рассаживания участников квартета и качество исполняемой ими музыки. Предикат Р ( х , у ) становится истинным лишь тогда, когда найдено такое взаимное расположение зверей в квартете, что качество музыки позволяет назвать исполнителей музыкантами. При этих условиях цитате из басни «Квартет» соответствует формула 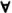x P( x , у ).

А вот Ф. Тютчев: «Бывают роковые дни лютейшего телесного недуга и страшных нравственных тревог…». Если Q ( u , v ) есть предикат, в котором переменная u определена на множестве дней, а переменная v на области настроений, связанных с «телесным недугом» и «страшными нравственными тревогами», то в исчислении предикатов началу стихотворения Тютчева будет соответствовать формула uQ ( u , v ).

Отметим, что имеют место следующие соотношения:

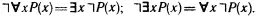
Справедливость их вытекает из смысла кванторов. Они позволяют любую формулу в исчислении предикатов представить в виде предваренной нормальной формы (ПНФ). В ней сначала выписываются все кванторы, а затем предикатные выражения. Например, формула

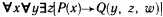
записана в ПНФ.

Введение кванторов 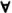и , а также их отрицаний наводит на мысль о связи исчисления предикатов и силлогистики Аристотеля. Вспомним еще раз смысл кванторов, использованных в силлогистике: Asp – «Всякое s есть р »; Esp – «Ни одно s не есть р », Isp – «Некоторые s есть р » и Osp – «Некоторые s не есть р ». Представляется вполне справедливым заменить эти выражения силлогистики следующими четырьмя формулами исчисления предикатов:

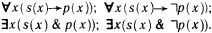
На первый взгляд такая замена вполне законна. Но для того, чтобы убедиться в этом, необходимо показать, что в исчислении предикатов могут быть выведены все модусы силлогистики Аристотеля.

Система аксиом и правила вывода в исчислении предикатов могут быть заданы следующим образом. В качестве системы аксиом берется любая известная система аксиом исчисления высказываний и к ней добавляются специфические для исчисления предикатов аксиомы, например, такие:

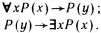
Смысл их очевиден. Первая аксиома говорит о том, что если Р ( х ) истинен для любых х , то и для некоторого у из того же универсума истинность предиката должна сохраняться. Вторая аксиома говорит о том, что если найдется такое у , что Р ( у ) будет истинным, то верно, что существует х , для которого Р ( х ) истинно.

К правилам вывода, используемым в исчислении высказываний, в исчислении предикатов добавляются еще три правила.

1. Пусть F 1и F 2– две формулы исчисления предикатов. И пусть в F 1переменная х не входит, а в F 2входит в качестве свободной переменной. Пусть, наконец, формула F 1 F 2является выводимой. Тогда выводима и формула F 1 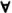xF 2.

2. Если х содержится в качестве свободной переменной в F 1и не содержится в таком виде в F 2и если F 1 F 2– выводимая формула, то 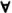xF 1 F 2также является выводимой.

3. Если F – выводимая формула и в F есть кванторы общности и существования, то любая из связанных ими переменных может быть заменена на другую связанную переменную одновременно во всех областях действий квантора и в самом кванторе. Полученная после этого формула также является выводимой.

Использование такой системы аксиом и такого множества правил вывода позволяет в исчислении предикатов из тождественно истинных формул получать тождественно истинные.

Вернемся теперь к попытке вложения силлогистических утверждений в исчисление предикатов. Исследование выводимости 24 модусов, верных в силлогистике Аристотеля, в исчислении предикатов привело к следующему результату. Если предполагать, что все классы сущностей непусты, т.е. рассуждения не касаются мыслимых сущностей (например, драконов или русалок), то приведенная выше замена силлогистических выражений выражениями логики предикатов будет полностью справедлива. Другими словами, при непустых классах сущностей все модусы силлогистики Аристотеля выводятся в исчислении предикатов.

Иная ситуация возникает при допущении пустых классов сущностей. В исчислении предикатов предикаты с пустыми областями для аргументов ведут себя совсем не так, как такие же предикаты с непустыми областями. В этих условиях оказываются невыводимыми все модусы силлогистики, в которых вывод носит частный характер, а обе посылки носят общий характер. Например, оказываются невыводимыми модусы AAI и ЕАО первой фигуры:

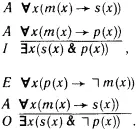
Хотелось бы обратить внимание читателей на только что полученный результат моделирования. Даже в области дедуктивных рассуждений, дающих всегда достоверные результаты, характер человеческих рассуждений может быть различным. И он не обязан совпадать (как это показывает случай с силлогистикой) с теми схемами рассуждений, которые демонстрирует исчисление предикатов.

Опишем общую схему выводов, лежащую в основе большого количества моделей человеческих достоверных рассуждений. Она приведена на рис. 19. Обратим сначала внимание на рис. 19, а . На нем показано некоторое дерево вывода . Вершинам этого дерева соответствуют определенные утверждения F i , а дуги определяют порядок получения новых утверждений. Те дуги, которые сходятся в зачерненные точки, образуют конъюнктивные условия вывода , а те дуги, которые между собой соединены «дужкой», образуют дизъюнктивные условия вывода . Например, получение утверждения F 9возможно двумя путями. Если доказаны утверждения F 2и F 3, то F 7следует из их доказанности, F 6из доказанности F 2и F 9из доказанности F 6и F 7. Другой путь доказательства F 9вытекает из априорной доказанности F 3или F 4. Любого из этих фактов достаточно для вывода F 8, который обеспечивает выводимость F 9.