Джеймс Гордон - Конструкции, или почему не ломаются вещи

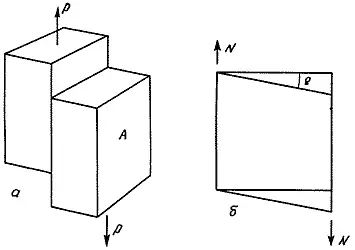
Рис. 118. Напряжение сдвига, или касательное напряжение, и деформация сдвига.

а - касательное напряжение = (перерезывающая сила / площадь) = Р/ А= τ .

б - деформация сдвига - это угол γ, на который искажается прямой угол в результате действия касательного напряжения τ.

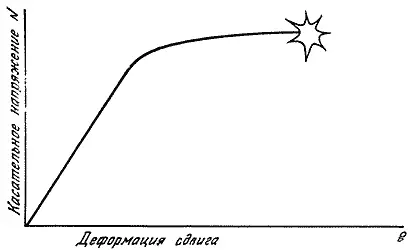
Рис. 119. Кривая деформирования при сдвиге похожа на соответствующую зависимость при растяжении.

Тангенс угла наклона прямолинейной части равен модулю сдвига: G = τ/ γ.

Для таких твердых тел, как металл, бетон или кость, упругая деформация сдвига обычно меньше 1° (1/57 радиана). При больших деформациях материалы этого типа либо разрушаются, либо испытывают необратимые пластические деформации - текут подобно сливочному маслу.

Однако такие материалы, как резина, текстильные ткани или мягкие биологические ткани, могут испытывать гораздо большие упругие и обратимые деформации сдвига - примерно до 30-40°. Для жидкостей и вязких материалов вроде патоки, крема или пластилина деформации сдвига не ограничены, но они и необратимы.

Модуль сдвига - G . Как и при растяжении, при малых и умеренных напряжениях большинство твердых тел следуют закону Гука при сдвиге. Так, построив график зависимости напряжения сдвига τот деформации γ, мы получим кривую, которая по крайней мере на ее начальном участке близка к прямой линии (рис. 119). Наклон этой прямой характеризует сдвиговую жесткость материала; тангенс угла наклона называется модулем сдвига. Он обозначается G . Таким образом,

модуль сдвига = (касательное напряжение / деформация сдвига)= τ/ γ= G

Модуль сдвига G аналогичен по смыслу модулю Юнга Е и, подобно последнему, имеет размерность единиц напряжения, например МН/м 2(кгс/мм 2) [89] Отметим, что между величинами G и Е существует связь. Для изотропных материалов, например для большинства металлов, G = E / 2(1 + ν) , где ν - коэффициент Пуассона. .

Как мы уже видели в предыдущей главе, хотя в верхней и нижней полках балки (или верхних и нижних стержнях фермы) возникают большие растягивающие или сжимающие напряжения (или усилия в стяжках), которые уравновешивают направленную вниз нагрузку и позволяют балке выполнять возложенную на нее миссию, - это напряжения сдвига, возникающие в стенке балки, соединяющей верхнюю и нижнюю ее полки. Стенка балки обычно представляет собой сплошную металлическую пластину, в ферме те же самые функции выполняет какая-либо решетчатая структура.

Так как между материалом и конструкцией нельзя провести четкой грани, то и здесь не очень важно, чем воспринимается перерезывающая сила в балке, сплошной ли стенкой или же решеткой, которая может быть из стержней, проволоки, деревянных брусьев или чего-либо другого. Правда, одно важное отличие здесь есть. Если стенка сделана, скажем, из металлической пластины, то не имеет никакого значения, под каким углом она была вырезана из большого листа, так как свойства металла по всем направлениям одинаковы. Такие материалы, а к ним относятся металлы, кирпич, бетон, стекло и большинство видов камня, называются изотропными, что по-гречески означает "одинаковые во всех направлениях", Тот факт, что металл изотропен (или почти изотропен) и имеет одинаковые по всем направлениям свойства, упрощает жизнь инженеров и объясняет их особое пристрастие к металлам.

Рассмотрим теперь стенку в виде решетки. Очевидно, что ее стержни должны располагаться под углом около +45° к оси балки. В противном случае стенка не будет иметь достаточной сдвиговой жесткости (рис. 120 и 121), под нагрузкой решетка сложится, и ферма скорее всего разрушится. Материалы, поведение которых напоминает поведение нашей решетки, называются анизотропными (или иногда аллотропными), что по-гречески означает "различные в различных направлениях".

Рис. 120. Сдвиг приводит к сжатию и растяжению под углом +45° к направлению сдвига.

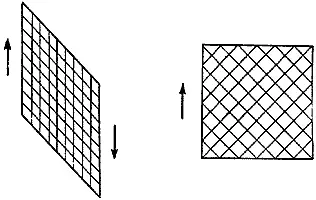
Рис. 121. Системы, подобные той, что изображена справа, являются жесткими на сдвиг, а системы, подобные изображенной слева, плохо ему сопротивляются.

Дерево, ткани и почти все биологические материалы анизотропны, причем каждый по-своему; это обстоятельство весьма усложняет жизнь, и не только инженерам. Ткань для одежды является самым распространенным рукотворным материалом, и она в высшей степени анизотропна. Как мы уже не раз говорили, различия между материалом и конструкцией довольно туманны, и ткань, хотя портные и называют ее материалом, на самом деле представляет собой конструкцию, состоящую из отдельных нитей, перекрещивающихся под прямым углом, и ведет себя при действии нагрузкой почти так же, как и решетчатая стенка балки или фермы.

Взяв в руки квадратный кусок обыкновенной ткани - это может быть носовой платок, - вы увидите, что в зависимости от направления приложенной растягивающей силы она деформируется совершенно по-разному. Если вы тянете строго вдоль нитей основы или утка [90] Нити основы идут параллельно длине рулона ткани, а нити утка переплетают их в перпендикулярном направлении. , ткань почти не растягивается; другими словами, ее жесткость на растяжение в этих направлениях велика. Более того, внимательно присмотревшись, вы заметите, что при этом сужение ткани в поперечном направлении тоже невелико (рис. 122), так что коэффициент Пуассона (о котором мы говорили в гл. 7 в связи с артериями) мал.

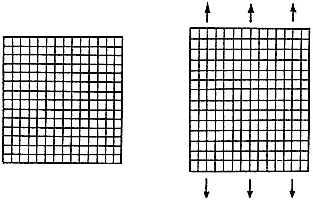
Рис. 122. При растяжении ткани параллельно нитям основы или утка материал оказывается жестким и его поперечное сокращение незначительно.

Но если вы теперь потянете ткань под углом 45° к направлению нити, то есть по диагонали, или, как говорят портные, "по косой", то она растянется гораздо больше; можно сказать, что в этом случае модуль Юнга весьма невелик. Одновременно произойдет большое поперечное сокращение, так что в этом направлении величина коэффициента Пуассона станет гораздо больше, а он может достигать величин порядка 1 (рис. 123). В целом же, чем более свободно соткана ткань, тем больше будет различие между ее поведением в диагональном и продольно-поперечном направлениях.