Николай Глинка - Общая химия

M 1= 2 · 22 = 44 г/моль

Нередко также молярную массу газа вычисляют, исходя из его плотности по воздуху. Хотя воздух представляет собой смесь нескольких газов, все же можно говорить о средней молярной массе воздуха, определенной из плотности воздуха по водороду. Найденная таким путем молярная масса воздуха равна 29 г/моль.

Обозначив плотность исследуемого газа по воздуху через D возд, получим следующее уравнение для вычисления молярных масс:

M 1= 29 D возд

Молярную массу вещества (а следовательно, и его относительную молекулярную массу) можно определить и другим способом, используя понятие о молярном объеме вещества в газообразном состоянии. Для этого находят объем, занимаемый при нормальных условиях определенной массой данного вещества в газообразном состоянии, а затем вычисляют массу 22,4 л этого вещества при тех же условиях. Полученная величина и выражает молярную массу вещества (в г/моль).

Пример.0,7924 г хлора при 0˚C и давлении 101,325 кПа занимают объем, равный 250 мл. Вычислить относительную молекулярную массу хлора.

Находим массу хлора, содержащегося в объеме 22,4 л (22 400 мл):

m = 22 400 · 0,724 / 250 ≈ 71 г

Следовательно, молярная масса хлора равна 71 г/моль, а относительная молекулярная масс хлора равна 71.

Измерения объемов газов обычно проводят при условиях, отличных от нормальных. Для приведения объема газа к нормальным условиям можно пользоваться уравнением, объединяющим газовые законы Бойля-Мариотта и Гей-Люссака

PV/T = P 0V 0/T 0

Здесь V — объем газа при давлении P и температуре T;

V 0— объем газа при нормальном давлении P 0(101,325 кПа или 760 мм рт. ст.) и температуре T 0(273 К)*.

* Точнее, 273,15 К.

- 28 -

Молярные массы газов можно вычислить также, пользуясь уравнением состояния идеального газа — уравнением Клапейрона — Менделеева

PV = mRT/M

где P — давление газа, Па; V — его объем, м 3; m — масса вещества, г; M — его молярная масса, г/моль; T — абсолютная температура, К; R — универсальная газовая постоянная, равная 8,314 Дж/(моль · К).

Если объем газа выражен в литрах, то управление Клапейрона-Менделеева приобретает вид

PV = 1000mRT/M

Описанными способами можно определять молекулярные массы не только газов, но и всех веществ, переходящих при нагревании (без разложения) в газообразное состояние. Для этого навеску исследуемого вещества превращают в пар и измеряют его объем, температуру и давление. Последующие вычисления производят так же, как и при определении молекулярных масс газов.

Молекулярные массы, определенные этими способами, не вполне точны, потому что рассмотренные газовые законы и уравнение Клапейрона-Менделеева строго справедливы лишь при очень малых давлениях (см. § 11). Более точно молекулярные массы вычисляют на основании данных анализа вещества (см. § 14).

При определении молекулярных масс газов очень часто приходится измерять объем газа, собранного над водой и потому насыщенного водяным паром. Определяя в этом случае давление газа, необходимо вводить поправку на парциальное давление водяного пара.

При обычных условиях различные газы смешиваются друг с другом в любых соотношениях. При этом каждый газ, входящий в состав смеси, характеризуется своим парциальным давлением . Оно представляет собой то давление, которое производило бы имеющееся в смеси количество данного газа, если бы оно одно занимало при той же температуре весь объем, занимаемый смесью.

Установленный Дальтоном закон парциальных давлений гласит:

Давление смеси газов, химически не взаимодействующих друг с другом, равно сумме парциальных давлений газов, составляющих смесь.

- 29 -

Пусть над водой собрано 570 мл газа при температуре 20˚C и давлении 104,1 кПа. Это давление складывается из двух величин — парциального давления самого газа и давления насыщенного водяного пара. Последнее при каждой температуре имеет вполне определенную величину, а частности при 20˚C оно равно 2,34 кПа (см. стр. 202). Следовательно, парциальное давление газа в данном случае равно 104,1-2,34 = 101,76 кПа. Приводя измеренный объем газа к нормальным условиям, следует подставить в уравнение не общее давление газовой смеси (104,1 кПа), а парциальное давление газа (101,76 кПа):

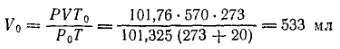
Если не учитывать поправку на давление паров воды, то вместо найденного объема получим

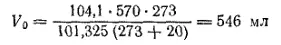
Ошибка составит 13 мл, т.е. 2,5%, что можно допустить только при ориентировочных расчетах.

Все рассмотренные газовые законы — закон Дальтона, закон простых объемных отношений Гей-Люссака и закон Авогадро, - приближенные законы. Они строго соблюдаются при очень малых давлениях, когда среднее расстояние между молекулами значительно больше их собственных размеров, и взаимодействие молекул друг с другом практически отсутствует. При обычных невысоких давлениях они соблюдаются приближенно, а при высоких давлениях наблюдаются большие отклонения от этих законов.

Из закона постоянства состава следует, что элементы соединяются друг с другом в строго определенных количественных соотношениях. Поэтому в химию были введены понятия эквивалента и эквивалентной массы ( слово «эквивалентный» в переводе означает «равноценный»).

В настоящее время эквивалентом элемента называют такое его количество, которое соединяется с 1 молем атомов водорода или замещает то же количество атомов водорода в химических реакциях . Например, в соединениях HCl, H 2S, NH 3, CH 4эквивалент хлора, серы, азота, углерода равен соответственно 1 моль, 1/2 моль, 1/3 моль, 1/4 моль.

Масса 1 эквивалента элемента называется его эквивалентной массой. Так, в приведенных выше примерах эквивалентные массы хлора, серы, азота, углерода соответственно равны 34,45 г/моль, 32/2 = 16 г/моль, 14/3 = 4,67 г/моль, 12/4 = 3 г/моль.

- 30 -

Эквиваленты и эквивалентные массы обычно находят либо по данным анализа соединений, либо на основании результатов замещения одного элемента другим. Для определения эквивалента (или эквивалентной массы) элемента необязательно исходить из его соединения с водородом. Эквивалент (эквивалентную массу можно вычислить по составу соединения данного элемента с любым другим, эквивалент (эквивалентная масса) которого известен.

Пример. При соединении 1,50 г натрия с избытком хлора образовалось 3,81 г хлора натрия. Найти эквивалентную массу натрия (Э Na) и его эквивалент, если известно, что эквивалентная масса хлора равна 35,45 г/моль.

Из данных задачи следует, что в хлориде натрия на 1,50 г натрия приходится 3,81 — 1,50 = 2,31 г хлора. Следовательно: