Андрей Варламов - Физика повседневности. От мыльных пузырей до квантовых технологий

Хорошо работая с квантовыми алгоритмами, квантовый компьютер сможет решить проблемы, которые слишком сложны для обычных последовательных компьютеров. Типичная проблема – поиск в телефонной книге имени абонента, номер которого известен. Поскольку список абонентов дан в алфавитном порядке, то для поиска без компьютера в среднем требуется время, пропорциональное их количеству N . Знакомый нам последовательный компьютер также нуждался бы во времени, пропорциональном N , пусть и с гораздо меньшим коэффициентом пропорциональности. Квантовый же компьютер благодаря способу вычисления (ученые говорят «алгоритм») индо-американского информатика Гровера затратил бы время, пропорциональное квадратному корню из числа N . Для больших N экономия времени существенна! Другой известный квантовый алгоритм (алгоритм Шора) позволяет раскладывать числа на простые множители. Эта проблема для обычного компьютера в случае больших чисел оказывается очень сложной, поэтому она лежит в основе системы шифрования RSA, повсеместно используемой для безопасности связи.

Будет ли квантовый компьютер в скором времени творить чудеса? К сожалению, на сегодняшний день существуют только простейшие версии квантовых процессоров, которые пока способны лишь демонстрировать возможность реализации упомянутых выше операций: например, идентифицировать один элемент из четырех с помощью алгоритма Гровера (илл. 10) или факторизовать целые числа… но только двузначные. Пока это можно куда лучше и дешевле сделать без квантового компьютера.

11. Пример квантового процессора с двумя кубитами. Эта сверхпроводящая схема (см. главу 24) позволяет реализовать алгоритм Гровера для идентификации одного элемента в наборе из четырех (как в телефонном справочнике, сокращенном до четырех абонентов). (Взято из диссертации Андреаса Дьюза, 2012, CEA Saclay)

Для разработки квантового компьютера требуется высочайший уровень технологий. Практическое создание необходимых для этого наноструктур подразумевает, что мы знаем не только то, как их делать, но и как их увидеть! Назовем четыре различных прибора, используемых для этого.

• Растровый электронный микроскоп, или РЭМ (илл. 12), дает трехмерные изображения нанообъектов с эффектом перспективы, как, например, на фотографии. Пучок электронов при сканировании проходит по поверхности образца, которая в ответ отражает электроны, излучает другие электроны, рентгеновские лучи, свет. Все эти частицы и волны, являющиеся носителями информации о материале и свойствах поверхности образца, анализируются микроскопом. Атомного разрешения РЭМ не достигает.

• Просвечивающий (трансмиссионный) электронный микроскоп, или ПЭМ (илл. 13). Он куда более громоздкий, чем РЭМ, зато способен достичь атомного разрешения. В этом случае для получения изображения анализируется пучок электронов, прошедший сквозь образец. Поэтому посредством просвечивающего микроскопа можно изучать только тонкие объекты. Если объект недостаточно тонок, его бы пришлось разрезать на пластины! Для нанообъектов эта деликатная операция не требуется.

• Сканирующий туннельный микроскоп, или СТМ. Это изобретение немца Герда Биннига и швейцарца Генриха Рорера, созданное в лаборатории IBM в Цюрихе (см. главу 24, «На берегу Цюрихского озера»), принесло им Нобелевскую премию в 1986 году, спустя пять лет после открытия. Это действительно удивительное изобретение, поскольку устройство способно «ощупывать» атомы с помощью иглы (илл. 14). На самом деле игла атома не касается: она приближается к нему на расстояние около 1 нм; при этом через зазор начинает течь туннельный ток (см. главу 25, «Квантование магнитного потока в сверхпроводящем кольце»). Расстояние от острия до атома должно выдерживаться с точностью до 0,1 нм, что означает, помимо прочего, что последнее должно быть надежно защищено от малейших колебаний. СТМ позволяет получить значительное атомное разрешение, однако он может передавать изображения только с самой поверхности твердого тела, следующий атомный слой остается невидимым (илл. 15). Кроме того, исследуемое вещество должно быть проводящим.

• Сканирующий атомно-силовой микроскоп, или АСМ. Подобно туннельному микроскопу, он «ощупывает» поверхности твердых тел с помощью иглы. Расстояние от кончика иглы до поверхности измеряется не по величине туннельного тока, а по силе, с которой поверхность действует на иглу. Последнюю определяют с помощью отклонения упругой консоли, которое регистрируется лазерным лучом. Поэтому вещество не обязательно должно быть проводящим (см. пример получаемого изображения в главе 19, «Полимеры»).

12. Электронный сканирующий микроскоп. На экране можно увидеть пример изображения

13. Просвечивающий электронный микроскоп

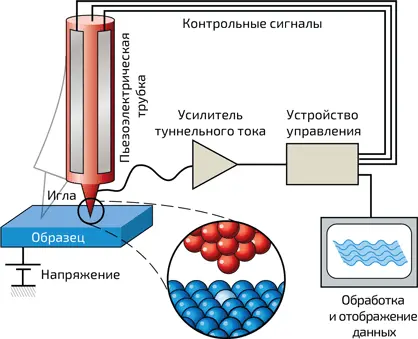
14. Схема действия туннельного микроскопа. Игла удерживается пьезоэлектрической трубкой на расстоянии приблизительно 1 нм от исследуемого образца. Туннельный ток усиливается и затем подвергается анализу

15. Пример изображения, полученного с помощью туннельного микроскопа. Это поверхность квазикристалла (см. главу 9, «Квазикристаллы»), которая обладает локальной симметрией пятого порядка

Наномир – королевство, где царят необычные физические законы. Это законы квантовой механики, и особенно они проявляют себя при низких температурах. Мы знаем, что энергия атома квантована, то есть может принимать только определенные значения, образующие дискретный набор. Оказывается, что при очень низкой температуре квантованным также является и сопротивление R очень маленькой электрической цепи! Напомним, что электрическое сопротивление в нашем обычном макроскопическом и относительно теплом мире главным образом обусловлено взаимодействием электронов с тепловыми колебаниями кристаллической решетки и ее дефектами (см. главу 24, «Природа электрического сопротивления»).

Правило этого квантования оказывается особенно простым, если говорить о величине, обратной сопротивлению, 1/ R , называемой кондактансом (или полной проводимостью). Она изменяется ступенчато, причем ее значение всегда является целым кратным 2e 2/h, где h – постоянная Планка. Уточним, как кондактанс можно менять: для этого в непосредственной близости от исследуемого объекта помещается электрод, называемый затвором (по аналогии с транзистором). Какого объекта? Обсудим два из них: квантовые провода и точечные контакты между полупроводниками.