Андрей Варламов - Физика повседневности. От мыльных пузырей до квантовых технологий

Квантовый провод представляет собой очень узкий проводящий канал (илл. 16), состоящий из кристаллического проводника без дефектов, диаметр которого сопоставим с длиной волны де Бройля (см. главу 22, «Волна де Бройля и уравнение Шрёдингера»). Узость канала обуславливает волновое поведение электронов, что проявляется квантованием их поперечного движения в проводе. В классическом проводнике траекторию движения электрона под воздействием разности потенциалов можно себе представлять как изломанную линию от одной примеси, на которой электрон рассеялся, до другой. Такое движение называют диффузным (илл. 17a). В квантовом же проводе распространение электрона является «баллистическим» (илл. 17b) и больше похоже на распространение электромагнитной волны в волноводе (см. главу 2, «Распространение звуковых волн»). Как только наименьший из размеров проводника сравнивается с дебройлевской длиной волны, электрон оказывается как бы «запертым» в этом направлении и ведет себя согласно законам квантовой механики. Можно сказать, что рассматриваемый нанопроводник становится «квантовой ямой», движение электрона в которой квантуется. Поскольку система находится вне равновесия, то речь идет не о квантовых состояниях, а о модах, по аналогии с модами волноводов. Изменяя электрический потенциал затвора (не показано на илл. 17), можно пропустить одну, две, три или более мод. Каждая мода вносит свой вклад в общую проводимость, определяемую суммой вкладов всех мод.

16. Изображение кремниевого квантового провода, полученное атомно-силовым микроскопом (АСМ) (экспериментальное устройство для измерения сопротивления). Тонкая часть провода имеет длину 1,5 мкм

Величина дебройлевской длины волны существенно зависит от концентрации электронов в металле. Для нормального металла она оказывается порядка нескольких ангстремов, то есть атомного масштаба. В полупроводниках, однако, эта величина может оказаться намного большей, и квантование движения электронов в таких нанопроводниках может существенно изменить их свойства по сравнению с массивными образцами, выполненными из того же материала. Например, квантование поперечного движения лишь в одном из направлений позволяет создать новый объект – двумерный электронный газ, который служит элементарным строительным блоком для современных электронных приборов.

Точечные контакты между полупроводниками обладают свойствами, сходными с квантовыми проводами. Сопротивление таких контактов можно варьировать при помощи изменения напряжения на затворе. В результате при низких температурах кондактанс изменяется ступеньками, величина которых кратна 2e 2/h.

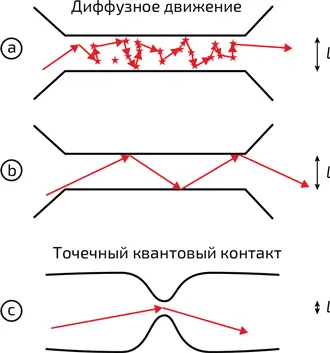
17. Движение электрона под действием приложенной разности потенциалов по проводу в зависимости от его ширины l .

a. Классический проводник. Траекторию электрона можно схематично представить как последовательность отрезков, соединяющих одну примесь с другой. Такое движение электрона называется диффузным.

b. Квантовый провод. Путь электрона можно представить в виде серии отражений от стенок.

c. Точечный квантовый контакт

Ярким проявлением квантования сопротивления является квантовый эффект Холла. В 1879 году американский физик Эдвин Холл (1855–1938) обнаружил новое явление. При прохождении тока через помещенный в магнитное поле B →проводник оно отклоняет электроны, и, таким образом, ток распространяется не только в направлении электрического поля x , но и в направлении y , перпендикулярном электрическому и магнитному полям (илл. 18a). В результате в этом направлении возникает разница потенциалов V y – так называемое холловское напряжение. Оно связано с текущим в направлении х током I x соотношением V y = R yx I x , коэффициентом в котором выступает так называемое сопротивление Холла R yx . Оно оказывается пропорциональным величине поля B →и обратно пропорциональным количеству носителей заряда на единицу объема. Таким образом, эффект Холла позволяет определить концентрацию носителей заряда, что весьма важно, в частности, для исследования свойств полупроводников.

Эффект, обнаруженный Холлом, имеет чисто классическую природу, за исключением случаев, когда выполняется три условия: низкая температура (в несколько кельвинов); сильное магнитное поле (около 20 Тл); и, наконец, движение электронов имеет двумерный характер. С ростом магнитного поля холловское сопротивление растет не линейно, а скачкообразно (илл. 18b). При этом значения его обратной величины – кондактанса – являются целыми кратными e 2/h.

А как создают такой необычный объект, как двумерный электронный газ? Метод, используемый в первом эксперименте по квантовому эффекту Холла, заключался в приложении сильного положительного потенциала (с помощью «затвора», вездесущего в нанофизике объекта) к поверхности кремния.

Квантовый эффект Холла, обнаруженный в 1980 году немецким ученым Клаусом фон Клитцингом в Лаборатории сильных магнитных полей в Гренобле, стал огромным достижением европейской науки. В 1985 году фон Клитцинг за это открытие получил Нобелевскую премию по физике.

Удивительным свойством квантового эффекта Холла является та точность, с которой выдерживается в квантовании кондактанса соотношение h/e 2= 25 812,807 Ом. Так, например, величина скачков между плато не зависит от чистоты образца. Начиная с 1990 года квантовый эффект Холла избран как способ определения эталона электрического сопротивления.

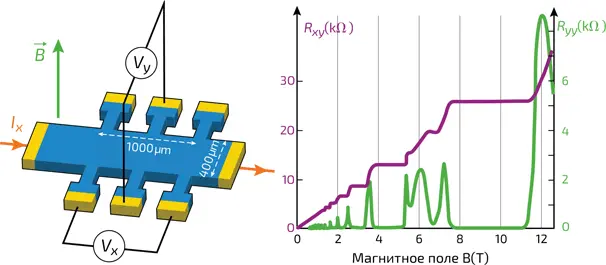
18. a.Схема опыта квантового эффекта Холла. b.Результат эксперимента. Кривая с пиками – сопротивление Холла R yx . На другом графике показана зависимость продольного сопротивление R yy от магнитного поля, которое, за исключением специальных точек, равно нулю

В этой главе мы обсудили сегодняшнее применение наноструктур в науке и технике. Также мы упомянули их некоторые замечательные фундаментальные свойства, которые пока еще изучаются в лабораториях, однако, весьма вероятно, найдут свои применения в будущем. Так, например, открытие квантования потока в сверхпроводниках позволило измерять очень слабые магнитные поля (см. главу 25, «Измерение очень слабых магнитных полей»), а квантование сопротивления в квантовом эффекте Холла – определить соотношение h/e 2с необычайной точностью.