Андрей Варламов - Физика повседневности. От мыльных пузырей до квантовых технологий

Представим, что стрелок находится на Северном полюсе, в точке N (илл. 4), и выпускает в направлении цели C, движущейся вместе с Землей, пулю P с начальной скоростью v . Земля вращается вокруг своей оси с угловой скоростью Ω, равной одному обороту в день. Таким образом, через некоторое время t она провернется на угол Ω t , и цель сдвинется вместе с ней. Тем не менее, с точки зрения стрелка, стоящего на Северном полюсе и глядящего на цель, все происходит так, будто бы последняя осталась на месте, а пуля отклонилась от заданной им траектории NC. Расстояние от P до линии NC в момент t составляет приблизительно произведение угла Ω t на пройденное пулей расстояние vt , то есть Ω vt 2. В этом рассмотрении мы считаем промежуток времени достаточно коротким, а угловую скорость Ω – измеренной в радианах в секунду.

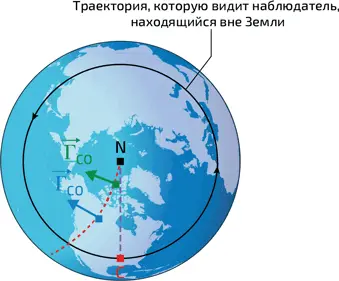
4. Отклонение пули под действием силы Кориолиса в системе отсчета, связанной с Землей. Пуля, выпущенная из ружья на Северном полюсе N в направлении цели C, отклоняется к западу от цели. Для наблюдателя вне Земли траектория пули – прямая линия (фиолетовая). Для наблюдателя, связанного с Землей, траектория представляется красной кривой (ее кривизна здесь сильно преувеличена): действующая на пулю сила Кориолиса придает ей ускорение Г → CO , показанное на рисунке в два разных момента

Таким образом, для достаточно малых промежутков времени пуля относительно Земли будет равномерно двигаться в направлении NC со скоростью v и в то же время равноускоренно двигаться вправо, в направлении, перпендикулярном отрезку NC (если бы стрельба производилась на Южном полюсе, то пуля отклонилась бы влево). При этом ускорение, называемое Кориолисовым, оказывается равным 2Ω v (вторая производная по времени от пройденного расстояния Ω vt 2). В соответствии со вторым законом Ньютона (см. главу 4, врезку «Ньютоновская механика»), это означает, что на пулю воздействует сила величиной 2Ω vm , сонаправленная ускорению Кориолиса. Это и есть сила Кориолиса .

Ускорение Кориолиса всегда перпендикулярно мгновенной скорости (илл. 4). Напомним, что в рассматриваемой задаче, благодаря действию силы тяжести, имеется еще и вертикальное ускорение, которое мы (в отличие от артиллеристов!) здесь не учитывали.

Уточним, что сила Кориолиса – сила «фиктивная», или, как часто говорят, сила инерции, потому что она не вызвана физическим воздействием одного тела на другое. При описании движения тела во вращающейся системе координат сила Кориолиса должна учитываться всегда, когда скорость тела не направлена вдоль оси вращения.

Прикинем, действительно ли стрелок промахнется мимо цели, если он не учтет силу Кориолиса? Предположим, что цель расположена на расстоянии d = 100 м, а скорость пули составляет v = 1000 м/с. Время, необходимое пуле для достижения цели, t = d/v = 0,1 с. Скорость вращения Земли составляет Ω = 2π радиан/день, что составляет около 0,7∙10 –4радиан/с. Тогда вызванное силой Кориолиса отклонение есть y = Ω vt 2= 0,7 мм. Таким образом, стрелок в рассматриваемом случае не промахнется. Он даже не поймет, что его цель двигалась относительно траектории пули. Можно также вычислить ускорение Кориолиса, равное 2Ω v : оно составляет 0,14 м/с 2.

В начале XVII века итальянский ученый Галилео Галилей (1564–1642) сделал первый шаг в понимании законов движения и гравитации. Он показал, что находящийся в свободном падении объект равномерно ускоряется, а также сформулировал принцип инерции: «Тело, которое не подвергается никакому воздействию, сохраняет свое движение по прямой линии с постоянной скоростью, если оно уже находится в движении, или остается неподвижным, если изначально находилось в состоянии покоя». Это утверждение кажется очевидным. Тем не менее со времен Аристотеля считалось, что для движения тела необходимо наличие внешнего воздействия. Вскоре, после Галилея, немецкий астроном Иоганн Кеплер (1571–1630) сформулировал законы, объясняющие движение планет. Первый из этих законов гласит, что планеты в своем движении вокруг Солнца описывают эллипсы, причем Солнце находится в одном из фокусов соответствующего эллипса. Позже англичанин Исаак Ньютон (1643–1727) заложил основы классической механики, основываясь на нескольких простых предположениях .

В качестве первого он принял принцип инерции Галилея. Второе предположение, или второй закон Ньютона, который часто называют основным законом динамики, гласит, что ускорение a →= dv →/ dt , приобретаемое материальной точкой и умноженное на ее массу m , равно сумме воздействующих на эту точку внешних сил F →:

Σ F → ext = ma →.

Этот закон дает нам основное уравнение движения и позволяет предсказать положение и скорость материальной точки в любой момент времени при условии, что мы знаем, где она находилась и какая у нее была скорость при t = 0.

Казалось бы, из второго закона Ньютона вытекает и первый, достаточно положить нулем сумму приложенных сил. Однако, принцип инерции имеет свой глубокий смысл, который придает ему статус закона. В современной формулировке он звучит так: «Существуют определенные системы отсчета, называемые галилеевыми , по отношению к которым движущийся объект сохраняет постоянную скорость, когда на него не действуют никакие силы, или сумма внешних сил равна нулю». Другими словами, первый закон Ньютона позволяет выбрать такие системы отсчета, в которых будут справедливы второй и третий законы.

Третий закон Ньютона, или принцип действия и противодействия, гласит: «При воздействии одного тела на другое первое испытывает ответное воздействие со стороны второго той же силы, но направленной противоположно».

И наконец, Ньютон сформулировал закон всемирного притяжения(или тяготения). Он научил будущие поколения, что два массивных тела притягиваются с силой, пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними (см. главу 5, «Ньютон – основатель современной физики»).

Законы механики Ньютона и сформулированный им закон всемирного тяготения с высокой точностью объяснили все проблемы механики, существовавшие в его время. Например, падение яблока на землю (см. илл. 2 в главе 5) и движение планет вокруг Солнца! Эти законы успешно применялись в астрономии для расчета траектории движения спутников вокруг планет и предсказали возвращение кометы Галлея в 1759 году. К сожалению, многие реальные проблемы часто настолько математически сложны, что возможно только их приблизительное решение. Это относится, например, к задаче о движении трех тел (скажем, Солнца, Земли и Луны) под воздействием взаимного гравитационного притяжения – ее точного решения просто не существует.