Грегори Гбур - Загадка падающей кошки и фундаментальная физика

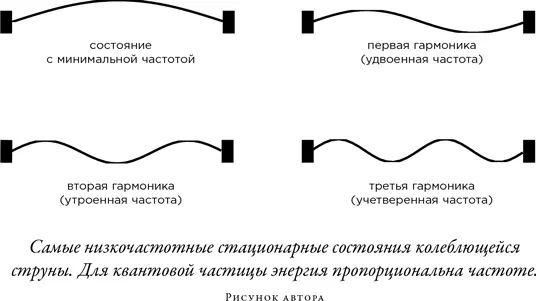
Квантовые частицы, или колеблющиеся волны, можно возбуждать и в «ящиках» более сложных форм. К примеру, волны возникают на круглой поверхности барабана, что аналогично квантовой частице, заключенной в круглый «ящик»; стационарные состояния для нее будут связаны с поверхностью барабана. Для «ящиков» простых форм, круглых или прямоугольных, мы можем математически вычислить энергии стационарных состояний; этим базовым вычислениям учат студентов-физиков.

Однако для «ящиков» более сложных форм вычисления часто не могут быть проделаны напрямую: нахождение стационарных состояний в них может оказаться очень трудным делом. В конце 1970-х гг. Майкл Берри из Университета Бристоля захотел разобраться в стационарных состояниях подобных случаев. В частности, он занимался поиском систем, в которых два или более стационарных состояния в конечном итоге имеют одинаковую энергию; такие ситуации называют вырожденными . Случаи вырождения в задачах, которые исследовал Берри, встречаются бесконечно редко; единственный способ найти их состоит в том, чтобы математически изучить одновременно весь класс систем и выделить в нем те системы, в которых происходит вырождение. Так каждый, кто ищет четырехлепестковый клевер, должен пересмотреть целое поле клевера, чтобы заметить нужный экземпляр среди куда более обычных трехлепестковых растений.

Задачей, исследованием которой занимался Берри, был случай с квантовой частицей, отражающейся от стенок треугольного «ящика», что аналогично волнам, колеблющимся на поверхности треугольного барабана {5} . Изучив стационарные состояния, возникающие во всех треугольных «ящиках», какие только можно вообразить, реально было бы найти те «ящики», в которых происходит вырождение. В контексте этой задачи случаи вырождения называются диаболическими точками — из-за их связи с фигурой в виде двойного конуса, напоминающей игрушку диаболо (а не из-за присущих им дьявольских свойств).

Форму треугольника можно охарактеризовать двумя параметрами, а именно двумя внутренними углами, которые мы обозначим X и Y . Поскольку все три угла любого треугольника в сумме дают 180°, третий угол при выборе двух остальных также фиксируется. Так что Берри и его коллега Марк Уилкинсон вывели математический метод поиска в «ящиках» диаболических точек с любыми возможными величинами X и Y . Но как они должны были узнавать о том, что диаболическая точка найдена? Ученые выявили одно любопытное свойство исследуемой системы. Поскольку в диаболической точке задействованы два различных стационарных состояния в пределах треугольника, обладающие в точности одинаковой энергией, Берри и Уилкинсон выяснили, что если математически «обойти» треугольник из их коллекции, рассматривая X и Y как широту и долготу пройденного пути, то волны двух стационарных состояний перевернутся «вниз головой» за время прогулки, если путь содержал диаболическую точку.

Здесь мы можем провести прямую аналогию с нашим многоуровневым гаражом. Точно так же как полярный исследователь, пройдя по пандусу, окажется на другом уровне гаража, так волны треугольника поменяют знак, если «обойти» вокруг диаболической точки: «верхняя» часть каждой волны станет «нижней», и наоборот. Ключевая разница состоит в том, что прогулка по пандусу гаража — это прогулка в реальном пространстве, тогда как «прогулка» Берри и Уилкинсона — это теоретическая прогулка по математическому конструкту. Воспользовавшись этой методикой, они нашли в своем множестве треугольников немалое число диаболических точек.

Изменение волны в данном случае верно было бы назвать топологической фазой . Топология — область математики, в которой объекты различаются по тому, как соединены составляющие их части; сфера, к примеру, отличается от бублика, потому что в бублике есть отверстие, а в сфере — нет. Многоуровневый паркинг, в свою очередь, отличается от множества уложенных друг на друга параллельных плоскостей, потому что в паркинге уровни связаны пандусами. В случае топологической фазы Берри и Уилкинсона максимальное изменение, которого можно было бы ожидать при переходе с одного «уровня» на другой, — это смена знака волны.

Эта топологическая фаза указывала на приближение глубокого прорывного открытия. «Момент зачатия», как называл его Берри, пришелся на весну 1983 г., когда он представил свою работу в Технологическом институте Джорджии. Берри и до этого замечал, что диаболические точки могут существовать только в случае, когда на частицу в треугольном «ящике» не действуют магнитные поля. Он продолжил мысль:

Таким образом, если к частице в треугольниках приложить слабое магнитное поле, диаболические точки должны исчезнуть. В конце лекции Рональд Фокс (в то время заведующий кафедрой физики) спросил, что происходит со сменой знака, когда включается магнитное поле.

Это был спусковой крючок, момент зачатия. Я немедленно ответил: «Полагаю, фаза изменяется на величину, отличную от π, — и тут же дал необдуманное обещание: — Я разберусь с этим сегодня и отвечу завтра». На самом деле потребовалось несколько недель, чтобы как следует разобраться в геометрической фазе {6} .

Берри понял, что квантовая частица, медленно прошедшая через цепочку изменений и приведенная вновь в первоначальные условия, может тем не менее оказаться при этом в состоянии, отличном от начального. Он показал также, что изменение, которое накапливается в этом процессе, зависит от базовой математической геометрии квантовой системы, о которой идет речь, то есть это геометрическая фаза . Берри наткнулся на неоцененную прежде общую черту многих квантовых систем. Свою работу он опубликовал в 1984 г. {7}

Предположим — в случае треугольного «ящика», — мы начинаем с электрона в «ящике» в форме равностороннего треугольника и прикладываем магнитное поле. Затем форма «ящика» медленно искажается таким образом, что суммарное изменение X и Y проводит его непрерывно через различные формы и приводит обратно в равносторонний вид. Берри показал, что, хотя «ящик» в конце возвращается в ту же форму, какую имел первоначально, окажется, что волна квантовой частицы при этом накопила другую фазу, значение которой связано с математической геометрией всего множества треугольных «ящиков».

Здесь, наконец, связь с маятником Фуко становится явной. В точности как маятник, пронесенный по замкнутой траектории вдоль широтной линии Земли, качается в направлении, отличном от начального, так и квантовая частица, пронесенная по замкнутому пути через некоторое множество изменений системного параметра, оказывается в состоянии, отличном от начального. И кошка, проделывая последовательность движений отдельными сегментами тела и возвращая тело в первоначальную форму, оказывается в конечном итоге в другой ориентации по сравнению с начальной. И задача падающей кошки, и маятник Фуко представляют собой примеры того накапливаемого изменения состояния, которое называют геометрической фазой.