Грегори Гбур - Загадка падающей кошки и фундаментальная физика

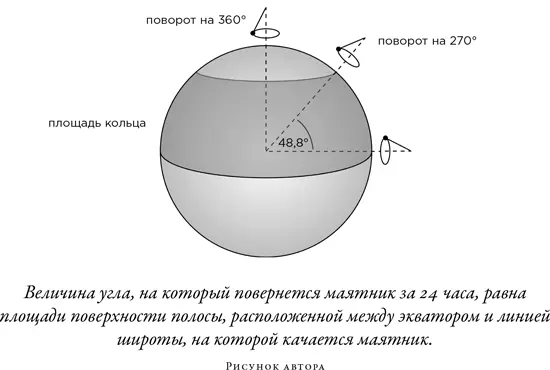
Задачу с кошкой также можно связать с площадью поверхности подходящей геометрической формы. Для кошки с конкретным отношением длины к обхвату в поясе мы можем описать ее ориентацию — геометрическую фазу — при помощи сферы {15} . Воспользовавшись моделью «сложись и крутись» Радемакера и тер Браака, мы можем сказать, что широта на сфере отражает степень сложения кошки в поясе, а долгота — степень ее скрученности, тоже в поясе; на иллюстрации можно увидеть, как мы находим соответствующую точку. Из этого следует, что любые действия кошки, любые ее повороты и закручивания можно изобразить в виде траектории на сфере и показать, что суммарный поворот кошки как целого при возвращении в нормальное положение равен площади поверхности, которую эта траектория описывает на этой «кошачьей сфере».

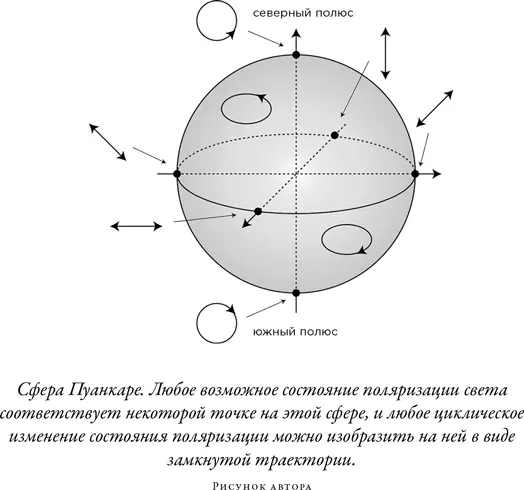
Таким образом, подлинная красота геометрической фазы состоит в том, что она позволяет решать очень сложные задачи через использование очень простой геометрии. Посмотрим еще раз на сложную модель переворачивания кошки Кейна и Шера, разработанную в конце 1960-х гг. для NASA. Серьезным ограничением более ранней модели Радемакера и тер Браака было предположение о том, что кошка сохраняет один и тот же изгиб позвоночника все время переворота, хотя совершенно очевидно, что кошка не может изгибаться назад так же хорошо, как вперед. В модели Кейна и Шера кошка уменьшает изгиб спины по мере закручивания и, по существу, в самой его середине резко меняет знак бокового изгиба.

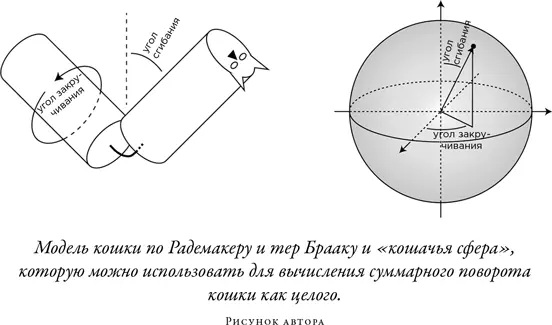
Если мы сравним оба варианта переворота на «кошачьей сфере», то увидим и ограничения модели Радемакера и тер Браака, и разумность модели Кейна и Шера. Взглянув на «кошачью сферу» сверху, мы увидим, что в простой модели Радемакера и тер Браака кошке придется очень сильно выгнуться назад. Напротив, модель Кейна и Шера позволяет избегать чрезмерного прогиба назад. Там кошка, прежде чем завершить движение, быстро переключается с изгиба вправо на изгиб влево.

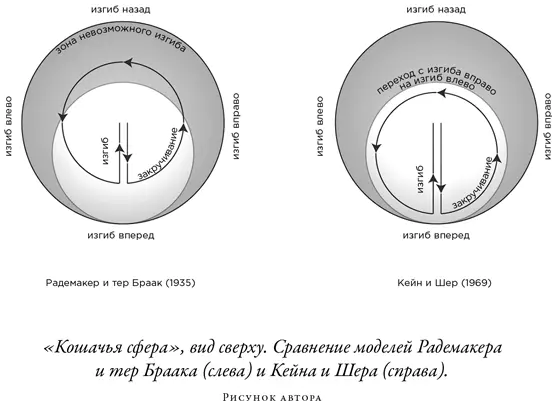
Понятно, что оптимальным выбором является модель Кейна и Шера: она позволяет окружить траекторией максимальную площадь (и, соответственно, получить максимальный переворот) и при этом не требует, чтобы позвоночник кошки сгибался под невозможными углами. С эволюционной точки зрения движение кошки отточено так, чтобы в максимальной степени использовать все доступные ей сгибания и закручивания.

Описание переворачивания кошки с использованием сферической поверхности вновь приводит нас по иронии судьбы к первоначальной работе Антуана Парана, проделанной более 300 лет назад. Круг замкнулся. Паран, исходя из соображений математического удобства, предложил рассматривать кошку как шар. И сегодня, рассматривая переворачивание кошки в контексте геометрической фазы, мы видим, что кошку и правда можно представить моделью в виде шара, хотя и совершенно иначе, чем представлял себе Паран.

Возможно, геометрическая фаза — последняя глубокая тайна, которую хранит падающая кошка. Хотя в 1980-е гг. геометрическая фаза была признана ученым сообществом как явление общего порядка, в 1894 г., когда Марей продемонстрировал свои фотографии падающей кошки в Парижской академии наук, она поставила ученых в тупик. Потребовалось около 100 лет, чтобы задача о падающей кошке была признана явлением, связанным с геометрической фазой: кошки отлично умеют прятать свои секреты.

Но действительно ли связь с геометрической фазой — последний секрет, который скрывали кошки? Исследователи продолжают находить все больше связей между падающими кошками и тонкими физическими проблемами. В 1993 г. Ричард Монтгомери написал статью о «калибровочной теории падающей кошки», в которой использовал для описания переворачивания кошки весьма и весьма хитроумную математику. За этой работой последовала статья Тосихиро Иваи 1999 г., в которой автор рассмотрел проблему поворотов с нулевым моментом импульса в контексте квантовой физики; он уделил падающей кошке должное внимание {16} .

Но самой головоломной стала статья с провокационным названием «Приземляются ли свободно падающие квантовые кошки на лапы?» {17} , написанная в 2015 г. мексиканскими исследователями. В ней авторы рассмотрели падение чисто квантово-механической кошки и обнаружили, что она может приземлиться в состоянии кота Шрёдингера — то есть одновременно в нормальном и в перевернутом состоянии.

С давних пор говорят, что у кошки девять жизней. Может оказаться, что и у физики падающих кошек осталась еще жизнь в запасе.

На протяжении всей книги мы видели бесчисленные примеры того, как кошек использовали в качестве всего лишь подопытных животных. В противовес этому довольно мрачному взгляду на научный прогресс стоит признать, что многие физики на протяжении всей истории поддерживали куда более дружеские отношения со своими знакомцами из царства кошачьих; для таких ученых домашние питомцы были лаборантами, музами, спутниками и даже соавторами научных работ. Мы завершим книгу рассказом о некоторых из этих замечательных творческих союзов.

Для начала позвольте развенчать легенду о том, что Исааку Ньютону принадлежат не только изменившие мир открытия, касающиеся движения и силы тяжести, но и изобретение дверцы для кошки.

Самого Ньютона по характеру тоже можно было счесть похожим на кота, ибо он был умен, неистов и склонен к злым шуткам, к тому же предпочитал в своих занятиях одиночество. В список грехов для исповеди, написанный им в возрасте 19 лет, Ньютон включил, к примеру, такой: «Угрожал отцу и матери Смит сжечь их вместе с домом» {1} . Ньютон был в плохих отношениях с отчимом, достопочтенным Барнабасом Смитом, и, очевидно, сердился на мать за повторное замужество.

История изобретения Ньютоном дверцы для кошки регулярно повторялась в книгах в XIX в. Приведем полностью один из колоритных ее вариантов:

Вы ведь знаете анекдот о том, как Колридж, Саути и Уордсворт вместе не смогли придумать, как снять хомут с головы лошади, а девочка-шотландка сделала это одним движением. Country Parson рассказывает нам анекдот поинтереснее этого, про сэра Исаака Ньютона; кстати говоря, этот анекдот мы больше нигде не встречали. У великого философа была домашняя кошка с котенком, которых он держал у себя в кабинете; устав открывать для них дверь, чтобы впустить их или выпустить, он натолкнулся на следующую идею. «Ньютон вырезал в двери большое отверстие для кошки, чтобы та могла входить и выходить, и маленькое — для котенка. При этом он не подумал о том, о чем вспомнил бы последний мужлан: большим отверстием, через которое проходила кошка, котенок тоже мог бы пользоваться. Проделав отверстия, сэр Ньютон с гордостью сел ждать, чтобы увидеть, как животные пройдут сквозь них в первый раз. Когда они поднялись с ковра перед камином, на котором лежали, великий ум остановил какие-то сложные вычисления, положил перо — и едва ли не величайший человек стал внимательно за ними наблюдать. Кошка с котенком подошли к двери и обнаружили, что там устроены для них удобства. Кошка прошла через большое отверстие, проделанное для нее в двери, и котенок тут же последовал за ней ЧЕРЕЗ ТО ЖЕ САМОЕ ОТВЕРСТИЕ». Поскольку министров постоянно обвиняют в отсутствии здравого смысла, они могут утешиться, обнаружив себя в одной компании с поэтами и философами. Однако неразвитость с практической стороны определенно ведет к потере, причем не только удобства, но и власти и влияния {2} .