Стивен Вайнберг - Первые три минуты [litres]

Электрон. Легчайшая из известных массивных частиц. Все химические свойства атомов и молекул определяются электрическим взаимодействием электронов с атомным ядром и друг с другом.

Электронвольт. Применяемая в атомной физике единица энергии, равная энергии, которую приобретает электрон, пройдя разность потенциалов в один вольт. Один электронвольт равен 1,60219 × 10 –12эрг.

Энергия покоя. Энергия покоящейся частицы, которая может высвободиться, если частица проаннигилирует. Вычисляется по формуле Эйнштейна: E = тс 2 .

Энтропия. Фундаментальная физическая величина статистической физики, характеризующая степень беспорядка в физической системе. В процессах, не нарушающих термодинамическое равновесие, энтропия сохраняется. Второй закон термодинамики гласит, что в любых процессах полная энтропия остается постоянной либо возрастает.

Эрг. Единица энергии в системе СГС (сантиметр-граммсекунда), равная кинетической энергии тела массой один грамм, перемещающегося со скоростью один сантиметр в секунду. Один эрг равен одной десятимиллионной (10 –7) джоуля.

Эффект Доплера. Изменение частоты сигнала, возникающее при относительном движении источника и приемника.

Ядерное равноправие. Парадигма, согласно которой все адроны одинаково фундаментальны.

Эти заметки предназначены для читателя, желающего вникнуть в математические выкладки, на которых зиждется описательное изложение материала данной книги. Их можно пропустить без ущерба для понимания сути.

Пусть гребни волны испускаются источником света через равные промежутки времени T. Если он удаляется от наблюдателя со скоростью V , то за время T , разделяющее два последовательных гребня, источник пройдет расстояние VT. Чтобы достичь наблюдателя, волна должна затратить дополнительное время VT/c, где с – скорость света. Таким образом, промежуток времени, через который наблюдатель регистрирует соседние гребни, равен

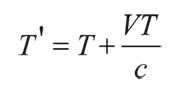
Длина волны испущенного света:

λ = cT .

Длина волны принимаемого света:

λ' = cT' .

Отношение этих длин:

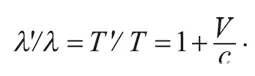
Предложенный вывод применим к случаю, когда источник движется по направлению к наблюдателю, за исключением того, что V меняется на – V . (Все вышесказанное справедливо в отношении любого волнового сигнала – не обязательно света.)

Например, скопления галактик в Деве удаляются от нас со скоростью 1000 км/с. Скорость света – 300 тысяч км/с. Следовательно, длина волны λ' любой из линий в спектре скопления больше ее номинального значения на коэффициент

Рассмотрим сферу радиуса R , заполненную галактиками. (Для наших целей R должно быть больше расстояния между скоплениями галактик, но меньше длины, сравнимой с размером Вселенной в целом.) Масса, заключенная в этой сфере, равна ее объему, умноженному на плотность вещества ρ:

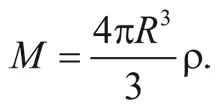
Согласно Ньютоновой теории всемирного тяготения, потенциальная энергия типичной галактики на поверхности этой сферы есть:

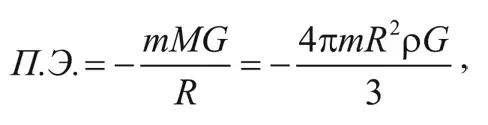
где m – масса галактики, а G – гравитационная постоянная Ньютона:

G = 6,67×10 –8см 3/(gm с 2).

Скорость этой галактики можно найти из закона Хаббла:

V = HR,

где H – постоянная Хаббла. Таким образом, кинетическая энергия равна:

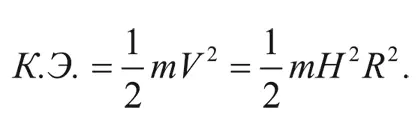
Полная энергия галактики – это сумма кинетической и потенциальной энергии:

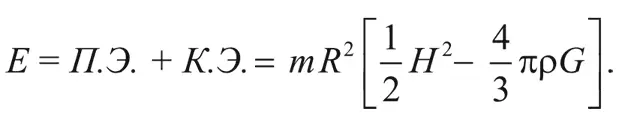
При расширении Вселенной эта величина должна оставаться неизменной.

Если E отрицательна, то галактика никогда не уйдет на бесконечность, поскольку на больших расстояниях потенциальной энергией можно пренебречь. Тогда полная энергия оказывается практически равной кинетической, а та, в свою очередь, всегда положительна. С другой стороны, если E положительна, то галактика может достичь бесконечности с некоторым запасом кинетической энергии. Таким образом, энергия E галактики, движущейся со скоростью убегания, по определению равна нулю. Откуда следует, что:

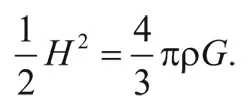
Другими словами, плотность должна равняться:

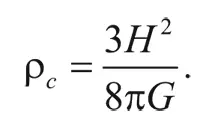
Это и есть критическая плотность. (Хотя мы получили этот результат в рамках ньютоновской физики, он применим и тогда, когда вещество во Вселенной обладает релятивистскими скоростями. Под ρ в таком случае понимается полная плотность энергии, деленная на с 2.)

Например, если взять общепринятое сегодня значение постоянной Хаббла (15 км/с на миллион световых лет), то, учитывая, что в световом годе 9,46 × 10 12километров, получим:

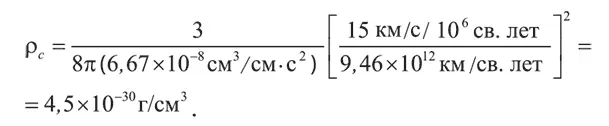
В одном грамме содержится 6,02 × 10 23нуклонов. Соответственно это значение критической плотности соответствует 2,7 × 10 –6нуклонам на кубический сантиметр, или 0,0027 частицы на литр.

Рассмотрим теперь, как параметры Вселенной меняются со временем. Допустим, в момент времени t типичная галактика массой m находится на расстоянии R(t) от произвольно выбранного центра – например, от нашей Галактики. В предыдущей заметке мы показали, что полная (кинетическая и потенциальная) энергия такой галактики равна:

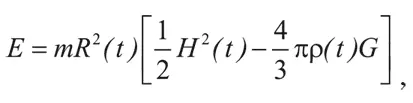
где H(t) и ρ( t ) – значения постоянной Хаббла и плотности вещества во Вселенной в момент времени t. Эта величина является постоянной. Однако мы скоро увидим, что ρ(t) при R(t) → 0 растет не медленнее, чем 1/ R 3 (t), поэтому ρ(t) R 2 (t) растет не медленнее, чем 1/ R(t), когда R(t) стремится к нулю. Чтобы результирующая энергия оставалась постоянной, два слагаемых в скобках должны быть почти равны. В итоге при R(t) → 0 имеем: