Джирл Уокер - Новый физический фейерверк

Если вы запускаете только один маятник, в системе возбуждаются обе моды и начинают конкурировать друг с другом. И тогда маятники колеблются с частотой, средней между частотами двух нормальных мод. Их амплитуда (размах каждого колебания) меняется с частотой, равной разности частот двух мод. Когда амплитуда одного маятника уменьшается, амплитуда другого увеличивается, и наоборот.

Аналогичный обмен движением происходит и в компасах, поскольку их стрелки колеблются относительно направления магнитного поля в точности так же, как маятники колеблются вокруг направления силы тяжести.

Подвесьте достаточно жесткую пружину за один конец, а к другому прикрепите грузик такого веса, чтобы пружина растянулась на треть и ее длина составила 4/3 от первоначальной. Потяните грузик вниз, а потом отпустите его. Сначала он будет колебаться в вертикальном направлении (рис. 1.42а), но вскоре эти колебания начнут превращаться в маятниковые (рис. 1.42б). Как только вертикальные колебания совсем прекратятся, маятниковое движение начнет затухать и опять появятся колебания грузика вдоль вертикали. Так и будет продолжаться: движение периодически будет меняться с одного вида (моды) на другой и обратно. Можно привести маятник в двухмодовый режим, если раскачать сначала не вертикальные колебания, а маятниковые.

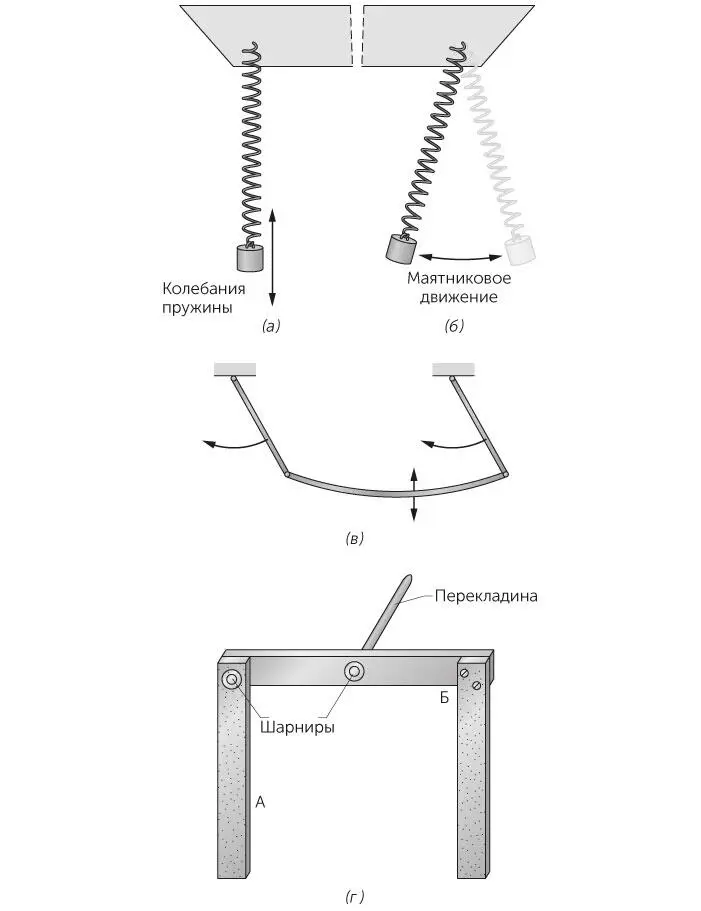
Рис. 1.42 / Задача 1.119.Чередование: а) вертикальных колебаний пружины и б) маятниковых колебаний. в) Чередование колебаний маятника и вертикальных колебаний соединяющего маятники упругого стержня. г) Чередование колебаний маятника А и Б.

Аналогичное чередование мод происходит в системе, изображенной на рис. 1.42в, в которой маятники соединены гибким стержнем. Стержень колеблется с частотой, удвоенной по сравнению с той, с которой колебался бы каждый из маятников, будь он свободным. В этом примере энергия переходит от колебаний маятников к колебаниям стержня.

Пример столь же сложной системы изображен на рис. 1.42 г. Горизонтальная планка может вращаться вокруг стержня, на котором держится вся конструкция. К одному концу этой планки жестко прикреплена вертикальная планка, а к другому — свободно вращающаяся на шарнире еще одна вертикальная планка. В этой конструкции имеется целых два маятника: маятник А — это вторая вертикальная планка, свободно висящая на горизонтальной планке, а маятник Б — система из горизонтальной планки и крепко к ней приделанной вертикальной планки. Если подогнать длины планок так, чтобы частота колебаний маятника А была равна удвоенной частоте колебаний маятника Б , и в начальный момент подтолкнуть маятник А , то возникнет периодическое чередование колебаний одного и другого маятников (рис. 1.41а).

Как в этих примерах объяснить чередование разных колебаний?

ОТВЕТ •Рассмотрим сначала первую систему. Если висящий на пружине груз сначала оттянуть, а потом отпустить, чтобы он отскочил строго по вертикали, пружина будет только сжиматься и разжиматься. Но так точно выдержать вертикальность невозможно — почти наверняка вы придадите ему некоторое движение вбок. Если подвесить грузик с параметрами, описанными в условии задачи, движение по вертикали будет происходить с частотой, удвоенной по сравнению с частотой чисто маятникового движения.

Предположим, что вначале грузик колеблется только в вертикальном направлении. Тогда начнется переход энергии от этой моды к маятниковой. Переход идет из-за того, что при вертикальных колебаниях меняется длина маятника. Ситуация та же, что и на детских качелях, на которых ребенок дважды встает и приседает за время одного полного колебания качелей. Ребенок при этом меняет эффективную длину качелей и тем самым вкачивает энергию в движущиеся качели — в результате они взлетают выше и выше.

Когда передача энергии к маятнику заканчивается, начинается обратный процесс, поскольку каждый раз, когда грузик проходит через точку максимальной высоты, он растягивает пружину. Это происходит дважды за полный цикл колебаний, так что его частота соответствует частоте вертикальных колебаний, и грузик опять начинает колебаться по вертикали. Но когда эти колебания становятся доминирующими, начинается перекачка энергии обратно в маятниковое движение. И так далее.

Когда в Кельнском соборе установили колокол и начали раскачивать его язык, колокол не зазвонил. Оказалось, что язык колебался с той же частотой, что и колокол, причем в фазе с ним, и просто не мог встретиться с внутренней поверхностью колокола. Как, по-вашему, следовало решать проблему, кроме как сбросить колокол с колокольни?

ОТВЕТ •Когда два маятника подвешены рядом и один из них короче и легче другого, они могут колебаться синфазно. Сам кельнский колокол был более длинным и массивным маятником, а его язык — более коротким и легким маятником, причем слишком коротким. После того как язык ударил по колоколу, он отскочил от него, подстроился под движение колокола, и оба маятника закачались в фазе. Больше столкновений между ними не происходило. Чтобы убрать эту синфазность, язык удлинили, при этом он стал массивнее и, ударяя по колоколу, начал двигаться медленнее и уже не в фазе с самим колоколом. И теперь, когда колокол на соборе качается, раздается колокольный звон.

Почему соус, в который вы окунули спагетти, разбрызгивается во все стороны, когда вы втягиваете длинную макаронину в рот? Это вызывает всеобщее веселье (а когда и неловкость) за столом, но оказывается, что эффектом спагетти интересуются и инженеры, проектирующие оборудование для производства бумаги. Этот эффект проявляется как при втягивании листов бумаги, так и при извлечении этих листов (так называемый обратный эффект спагетти ).

ОТВЕТ •Вот вам одно объяснение эффекта. Предположим, макаронина уже покинула тарелку и движется ко рту. В этот момент ее скорость может иметь и боковую составляющую. Если вы ее втягиваете в себя с постоянной скоростью, длина свободной части уменьшается, а соответственно, кинетическая энергия, связанная с боковой скоростью, сосредотачивается теперь в этом отрезке малой массы. Так как количество кинетической энергии не меняется, скорость бокового движения должна увеличиться. Когда свободный конец макаронины приближается к губам, скорость его становится настолько большой, что соус разбрызгивается во все стороны.

Другое объяснение основывается на понятии углового момента. Если свободный конец макаронины вращается вокруг точки ее касания губами, скорость вращения должна увеличиваться по мере втягивания ее в рот. Это напоминает фигуриста, который раскручивается с расставленными руками, а потом прижимает их к телу, чтобы крутиться быстрее.