Ричард Фейнман - Том 2. Электромагнетизм и материя

Так что если ядро находится в пустом пространстве в отсутствие внешних полей, то у него имеются четыре возможных состояния, каждое с одной и той же энергией. Для системы со спином 2 z -компонента момента количества движения принимает в единицах ℏ только следующие значения:

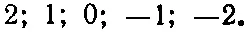
Если вы подсчитаете, сколько возможно состояний для данного спина j , то их получится (2 j +1). Другими словами, если вы скажете мне, какова энергия системы и ее спин j , то число состояний с этой же энергией в точности будет равно (2 j +1), причем каждое из них соответствует одной из различных величин z -компоненты момента количества движения.

Мне хотелось бы прибавить еще один факт. Если вы случайно выберете некоторый атом с известным j и измерите его z -компоненту момента количества движения, то сможете получить какое-то одно из возможных значений, причем каждое из них равновероятно . Любое состояние может характеризоваться только одним из возможных значений, но каждое из них столь же хорошо, как и любое другое. Каждое из них имеет в мире один и тот же вес (мы предполагаем, что никакой предварительной «сортировки» не было).

Кстати, этот факт имеет простой классический аналог. Представьте, что тот же самый вопрос вас интересует с классической точки зрения: какова вероятность какого-то определенного значения z -компоненты момента количества движения, если из набора систем, имеющих один и тот же момент количества движения, вы наугад выбрали одну? Ответ : любое из значений от максимального до минимального равновероятно (в чем вы можете легко убедиться сами). Этот классический результат соответствует равной вероятности любой из (2 j +1) возможностей в квантовой механике.

Из того, что у нас было до сих пор, можно получить другое интересное и в каком-то смысле удивительное заключение. В некоторых классических расчетах в окончательном результате появлялась величина, равная квадрату момента количества движения J, другими словами, J· J. И вот оказывается, что правильную квантовомеханическую формулу можно угадать с помощью классических вычислений и следующего простого правила: замените J 2= J· Jна j(j+1)ℏ 2. Этим правилом часто пользуются, и обычно оно дает верный результат, однако не всегда . Чтобы показать вам, почему это правило может хорошо работать, я приведу следующее рассуждение.

Скалярное произведение J· Jможно записать как

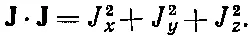
Поскольку это скаляр, то он должен оставаться одним и тем же для любой ориентации спина. Предположим, что мы случайно выбрали образец какой-либо атомной системы и произвели измерения либо величины J x 2, либо J y 2, либо J z 2— среднее значение любой из них должно быть тем же самым. (Ни одно из направлений не имеет особого преимущества перед любым другим.) Следовательно, среднее значение J· Jравно просто утроенной средней величине любой компоненты, скажем J z 2:

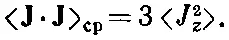
Но поскольку J· Jпри любой ориентации одно и то же, его среднее, разумеется, будет постоянной величиной

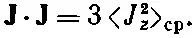(34.24)

Если же мы теперь скажем, что то же самое уравнение будет использоваться и в квантовой механике, то можем легко найти z 2> ср. Нам просто нужно взять сумму (2j+1) возможных значений J z 2и поделить ее на число всех значений:

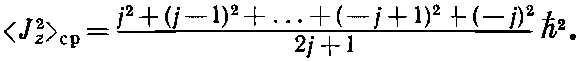(34.25)

Вот что получается для системы со спином 3/ 2:

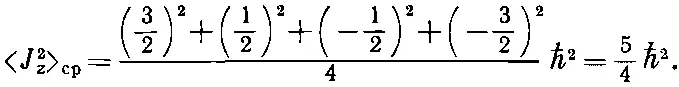
Отсюда мы заключаем, что

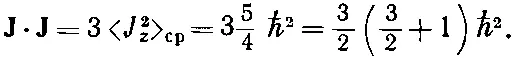
На вашу долю остается доказать, что соотношение (34.25) вместе с (34.24) дает в результате

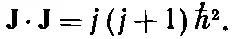(34.26)

Хотя в рамках классической физики мы бы думали, что наибольшее возможное значение z -компоненты Jравно просто абсолютной величине J, именно √( J· J), в квантовой механике максимальное значение J z всегда немного меньше его, ибо jℏ всегда меньше √( j ( j +1))ℏ. Момент количества движения никогда не направлен «полностью вдоль оси z».

Теперь я снова хочу поговорить о магнитном моменте. Я уже говорил, что в квантовой механике магнитный момент атомной системы может быть связан с моментом количества движения соотношением (34.6):

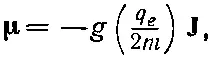(34.27)

где - q e —заряд, а m — масса электрона.

Атомные магнитики, будучи помещены во внешнее магнитное поле, приобретут дополнительную магнитную энергию, которая зависит от компоненты их магнитного момента в направлении поля. Мы знаем, что

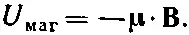(34.28)

Выбирая ось z вдоль направления поля В, получаем

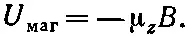(34.29)

А используя уравнение (34.27), находим

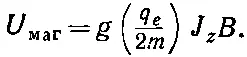
Согласно квантовой механике, величина J z может принимать только такие значения: jℏ, ( j -1)ℏ,...,- jℏ . Поэтому магнитная энергия атомной системы не произвольна, допустимы только некоторые ее значения. Например, максимальная величина энергии равна

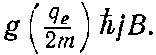
Величину q e ℏ /2 m обычно называют «магнетоном Бора» и обозначают через μ B :