Ричард Фейнман - Том 2. Электромагнетизм и материя

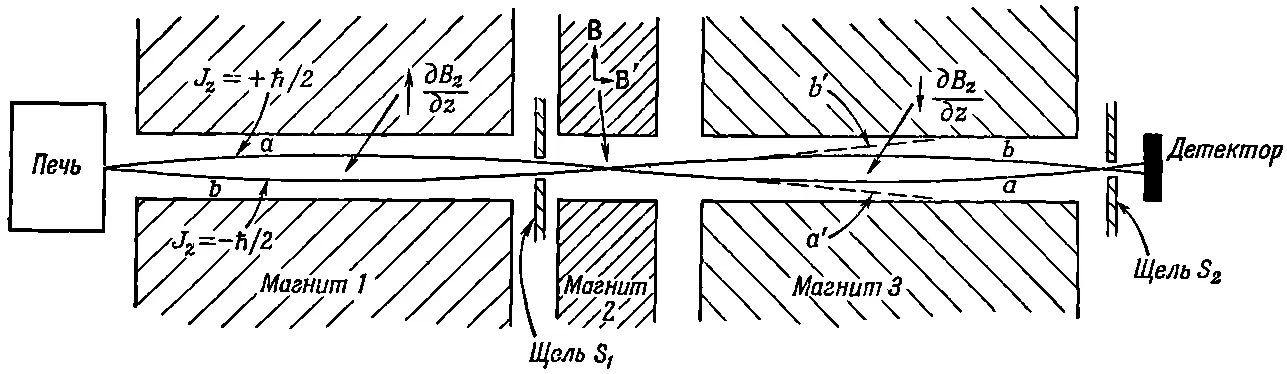
Фиг. 35.5. Схема установки Раби в опытах с молекулярными пучками.

Вы видите здесь печь, которая создает поток нейтральных атомов, летящих по прямому пути через три магнита. Магнит 1 — такой же, как и на фиг. 35.2, он создает поле с большим, скажем положительным, градиентом ∂ B z /∂ z . Если атомы обладают магнитным моментом, то они будут отклоняться вниз при J z=+ℏ/2 или вверх при J z=-ℏ/2 (поскольку для электронов μ направлен противоположно J). Если мы будем рассматривать только те атомы, которые могут проходить через щель S 1, то, как это показано на фиг. 35.5, возможны две траектории. Чтобы попасть в щель, атомы с J z=+ℏ/2 должны лететь по кривой а , а атомы с J z=-ℏ/2 — по кривой b . Атомы, вылетающие из печи в другом направлении, вообще не попадут в щель.

Магнит 2 создает однородное поле. В этой области на атомы никакие силы не действуют, поэтому они просто пролетают через нее и попадают в магнит 3. Этот магнит представляет собой копию магнита 1, но с перевернутым полем, так что у него ∂ B z /∂ z имеет отрицательный знак. Атомы с J z=+ℏ/2 (будем говорить «со спином, направленным вверх»), которые в магните 1 отклонялись вниз , в магните 3 будут отклоняться вверх ; они продолжат свой полет по траектории а и через щель S 2попадут в детектор. Атомы с J z=-ℏ/2 («со спином, направленным вниз») в магнитах 1 и 3 тоже будут испытывать действие противоположных сил и полетят по траектории b , которая через щель S 2тоже приведет их в детектор.

Детектор можно сделать разными способами в зависимости от измеряемых атомов. Так, для щелочных металлов, подобных натрию, детектором может служить тонкая раскаленная вольфрамовая нить, подсоединенная к чувствительному гальванометру. Атомы натрия, оседая на этой нити, испаряются в виде ионов Na +и оставляют на ней электрон. Возникает ток, пропорциональный числу осевших в 1 сек атомов натрия.

В щели магнита 2 находится набор катушек, которые создают небольшое горизонтальное магнитное поле В'.Эти катушки питаются током, осциллирующим с переменной частотой ω, так что между полюсами магнита 2 создается сильное вертикальное магнитное поле В 0и слабое осциллирующее горизонтальное магнитное поле В'.

Предположим теперь, что частота ω осциллирующего поля подобрана равной ω p— частоте «прецессии» атомов в поле В 0. Переменное поле вызовет у некоторых из пролетающих атомов переход от одного значения J z к другому. Атомы, спины которых были первоначально направлены вверх (J z=+ℏ/2), могут перевернуться вниз (J z=-ℏ/2). Теперь магнитный момент этих атомов перевернут, так что в магните 3 они будут чувствовать силу, направленную вниз , и полетят по траектории а', как показано на фиг. 35.5. Теперь они уже не смогут пройти через щель S 2и попасть в детектор. Точно так же некоторые из атомов, спин которых был первоначально направлен вниз (J z=-ℏ/2), перевернутся при прохождении через магнит 2 вверх (J z=+ℏ/2). После этого они полетят по траектории b ' и не попадут в детектор.

Если частота осциллирующего поля В'значительно отличается от ω pоно не сможет вызвать переворачивания спина и атомы по своим «невозмущенным» орбитам пройдут прямо к детектору. Итак, как видите, можно найти частоту «прецессии» атомов ω pв поле В 0 ,подбирая частоту ω магнитного поля В', пока не получим уменьшения тока атомов, приходящих в детектор. Уменьшение тока будет происходить тогда, когда ω попадет «в резонанс» с ω p . График зависимости тока в детекторе от ω может напоминать кривую, изображенную на фиг. 35.6.

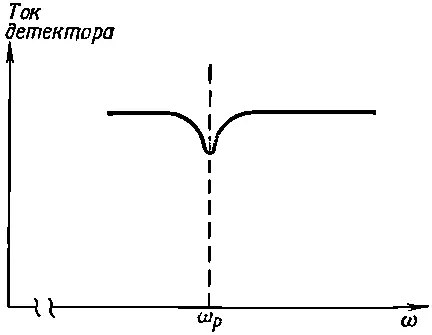
Фиг. 35.6. Количество атомов в пучке при ω=ω p уменьшается.

Зная ω, можно найти величину g для данного атома.

Такой резонансный эксперимент с атомными или, как их часто называют, «молекулярными» пучками представляет очень красивый и точный способ измерения магнитных свойств атомных объектов. Резонансную частоту ω pможно определить с очень большой точностью, по сути дела значительно точнее, нежели мы способны измерить поле В 0 ,необходимое при нахождении g .

Теперь мне бы хотелось описать явление парамагнетизма вещества. Предположим, имеется вещество, в составе которого имеются атомы, обладающие постоянным магнитным моментом, например кристаллы медного купороса. В этих кристаллах содержатся ионы меди, у которых электроны на внутренних оболочках имеют суммарный момент количества движения и магнитный момент, не равные нулю. Таким образом, ионы меди будут источником постоянного магнитного момента молекул купороса. Буквально несколько слов о том, какие атомы имеют постоянный магнитный момент, а какие — нет. Любой атом, у которого число электронов нечетно , подобно натрию, например, будет иметь магнитный момент. На незаполненной оболочке натрия имеется один электрон. Этот электрон и определяет спин и магнитный момент атома. Однако обычно при образовании соединения этот дополнительный электрон на внешней оболочке спаривается с другим электроном, направление спина которого в точности противоположно, так что все моменты количества движения и магнитные моменты валентных электронов в точности компенсируют друг друга. Вот почему молекулы, вообще говоря, не обладают магнитным моментом. Конечно, если у вас есть газ атомов натрия, то там такой компенсации не происходит [46] Обычные пары натрия в основном моноатомны, хотя изредка там и встречаются молекулы Na 2 . . Точно так же если у вас есть то, что в химии называется «свободным радикалом», т. е. объект с нечетным числом валентных электронов, то связи оказываются неполностью насыщенными и появляется ненулевой момент количества движения.

У подавляющего большинства материалов полный магнитный момент появляется только тогда, когда там присутствуют атомы с незаполненной внутренней электронной оболочкой. Благодаря этому они могут иметь суммарный момент количества движения и магнитный момент. Такие атомы принадлежат к «переходным элементам» периодической таблицы Менделеева, например: хром, марганец, железо, никель, кобальт, палладий и платина — элементы как раз такого сорта. Кроме того, все редкоземельные элементы имеют незаполненную внутреннюю оболочку, а следовательно, и постоянные магнитные моменты. Правда, встречаются еще странные вещества (к числу их относятся жидкий кислород и окись азота), которые, оказывается, тоже обладают магнитным моментом, но объяснить причины этих странностей я предоставляю химикам.