Ричард Фейнман - Том 2. Электромагнетизм и материя

Подчеркнем, что этот результат относится только к полю, созданному зарядами, размещенными на плоскости. Если по соседству есть другие заряды, общее поле близ плоскости было бы суммой (5.3) и поля прочих зарядов. Закон Гаусса тогда только гарантировал бы, что

(5.4)

где E 1и Е 2— поля, направленные на каждой стороне плоскости наружу от нее.

Задача о двух параллельных плоскостях с равными и противоположными плотностями зарядов +σ и -σ решается тоже просто, если только снова предположить, что внешний мир абсолютно симметричен. Составите ли вы суперпозицию двух решений для отдельных плоскостей или построите гауссов ящик, охватывающий обе плоскости, в обоих случаях легко видеть, что поле снаружи плоскостей равно нулю (фиг. 5.7, а ). Но, заключив в ящик только одну или только другую поверхность, как показано на фиг. 5.7, б или в , мы легко обнаружим, что поле между плоскостями должно быть вдвое больше поля отдельной плоскости.

Фиг .5.7. Поле между двумя заряженными листами равно σ/ε 0 .

Итог таков:

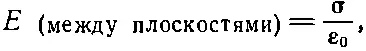(5.5)

(5.6)

В гл. 4 мы уже применяли закон Гаусса, когда должны были найти поле вне однородно заряженной шаровой области. Тот же метод может дать нам и поле в точках внутри шара. Этот расчет, например, может быть использован для получения хорошего приближения к полю внутри атомного ядра. Вопреки тому, что протоны в ядре взаимно отталкиваются, они из-за сильного ядерного притяжения распределены по всему ядру почти однородно.

Пусть у нас имеется сфера радиуса R , однородно наполненная зарядами. Пусть заряд в единице объема равен ρ. Снова, используя соображения симметрии, можно предположить, что поле радиально и в точках, равноудаленных от центра, по величине одинаково. Чтобы определить поле в точке на расстоянии r от центра, представим сферическую гауссову поверхность радиуса r (r

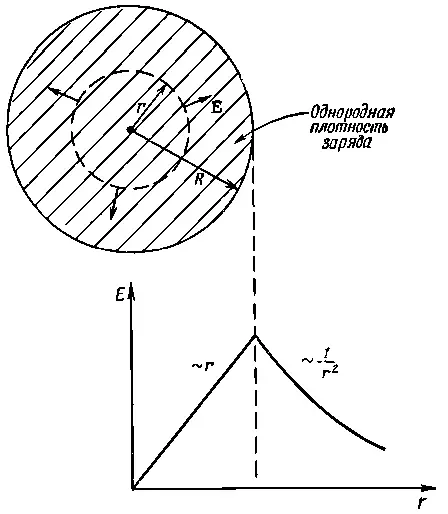
Фиг. 5.8. Закон Гаусса можно применить для определения поля внутри однородно заряженного шара.

Поток из нее равен

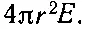
Заряд внутри нее равен внутреннему объему, умноженному на ρ, т. е.

Применяя закон Гаусса, получаем величину поля

(5.7)

Вы видите, что при r = R эта формула дает правильный результат. Электрическое поле пропорционально расстоянию от центра и направлено по радиусу наружу.

Аргументы, которые мы только что приводили для однородно заряженного шара, можно применить и к заряженной сфере. Опять предполагая радиальность и сферическую симметрию поля, из закона Гаусса немедленно получаем, что поле вне сферы во всем подобно полю точечного заряда, поле же внутри сферы — нуль (если мы проведем гауссову поверхность внутри сферы, то внутри нее зарядов не окажется).

Если мы вглядимся чуть пристальнее в то, как поле внутри сферы оказывается нулевым, то лучше поймем, почему закон Гаусса обязан своим происхождением закону Кулона, т. е. точной зависимости силы от второй степени расстояния. Возьмем произвольную точку Р внутри однородно заряженной сферической поверхности. Представим узкий конус, который начинается в точке Р и тянется до поверхности сферы, вырезая там небольшой сферический участок Δa 1(фиг. 5.9).

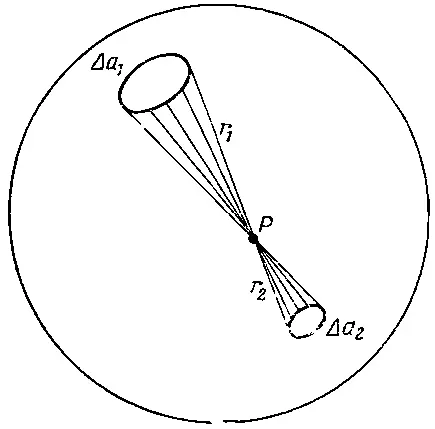
Фиг. 5.9. Во всякой точке Р внутри заряженной сферической оболочки поле равно нулю.

В точности симметричный конус по другую сторону вершины вырежет на поверхности площадь Δа 2. Если расстояния от Р до этих двух элементов площади равны r 1и r 2, то площади находятся в отношении

(Вы можете доказать это для любой точки шара с помощью геометрии.)

Если поверхность сферы заряжена равномерно, то заряд Δ q на каждом элементе поверхности пропорционален его площади

Тогда закон Кулона утверждает, что величины полей, создаваемых в Р этими двумя элементами поверхности, находятся в отношении

Поля в точности взаимно уничтожаются. Таким способом можно разбить на пары всю сферу. Значит, все поле в точке Р равно нулю. Но вы видите, что этого не было бы, окажись показатель степени r в законе Кулона не равным в точности двойке.

Справедливость закона Гаусса зависит от закона обратных квадратов Кулона. Если бы закон силы не подчинялся в точности зависимости 1/r 2, то поле внутри однородно заряженной сферы не было бы в точности равно нулю. Например, если бы поле менялось быстрее (скажем, как 1/r 3), то часть сферы, которая ближе к точке Р, создала бы в точке Р более сильное поле, чем дальняя часть. Получилось бы (для положительного поверхностного заряда) радиальное поле, направленное к центру. Эти заключения подсказывают нам элегантный путь проверки точности выполнения закона обратных квадратов. Для этого нужно только узнать, в точности ли поле внутри однородно заряженной сферы равно нулю.

Наше счастье, что такой способ существует. Ведь обычно трудно измерить физическую величину с высокой точностью. Добиться однопроцентной точности было бы нетрудно, но как быть, если нам понадобится измерить закон Кулона с точностью, скажем, до одной миллиардной? Можно почти ручаться, что измерить с такой точностью силу , действующую между двумя заряженными телами, не способны даже лучшие приборы. Но если только нужно убедиться в том, что поле внутри сферы меньше некоторого значения, то можно провести довольно точное измерение справедливости закона Гаусса и тем самым проверить обратную квадратичную зависимость в законе Кулона. В сущности происходит сравнение закона силы с идеальным законом обратных квадратов. Именно такие сравнения одинаковых, или почти одинаковых, вещей обычно становятся основой самых точных физических измерений.