Ричард Фейнман - Том 3. Квантовая механика

Начну с того, что напомню вам кое-какие свойства уравнения Шредингера [87] Фактически это не напоминание, потому что некоторые из этих уравнений я раньше не приводил; не забудьте, что я веду настоящий семинар. . Я хочу с помощью уравнения Шредингера описать поведение частицы в магнитном поле, потому что явления сверхпроводимости связаны с магнитными полями. Внешнее магнитное поле описывается векторным потенциалом, и вопрос состоит в том, каковы законы квантовой механики в поле векторного потенциала. Принцип, определяющий квантовомеханическое поведение частицы в поле векторного потенциала, очень прост.

Фиг. 19.1. Амплитуда перехода из а в b по пути r пропорциональна exp[(-iq/ℏ)∫Ads].

Амплитуда того, что частица при наличии поля перейдет по некоторому пути из одного места в другое (фиг. 19.1), равна амплитуде того, что она прошла бы по этому пути без поля, умноженной на экспоненту от криволинейного интеграла от векторного потенциала, умноженного в свою очередь на электрический заряд и деленного на постоянную Планка [см. гл. 15, § 2 (вып. 6)]:

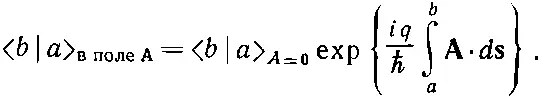(19.1)

Это исходное утверждение квантовой механики.

И вот в отсутствие векторного потенциала уравнение Шредингера для заряженной частицы (нерелятивистской, без спина) имеет вид

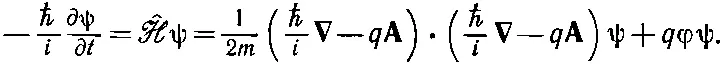(19.2)

где φ — электрический потенциал, так что q φ — потенциальная энергия [88] Только, пожалуйста, не путайте это φ с нашим прежним обозначением состояния φ ! . А уравнение (19.1) равнозначно утверждению, что в магнитном поле градиенты в гамильтониане нужно каждый раз заменять на градиент минус ( iq / ℏ ) А, так что (19.2) превращается в

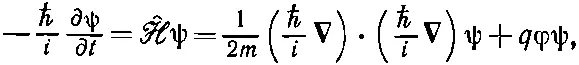(19.3)

Это и есть уравнение Шредингера для частицы с зарядом q (нерелятивистской, без спина), движущейся в электромагнитном поле А, φ.

Чтобы стало ясно, что оно правильно, я хочу проиллюстрировать это простым примером, когда вместо непрерывного случая имеется линия атомов, расставленных на оси x на расстоянии b друг от друга, и существует амплитуда — К того, что электрон перепрыгнет в отсутствие поля от одного атома к другому [89] К — это та самая величина, которая в задаче о линейной решетке обозначалась буквой А (см. гл. 11). . Тогда, согласно уравнению (19.1), если имеется вектор-потенциал А x ( х, t ) в x -направлении, то амплитуда перескока по сравнению с тем, что было раньше, изменится, ее придется домножить на exp[( iq / ℏ ) A x b ] — экспоненту с показателем, равным произведению iq / ℏ на векторный потенциал, проинтегрированный от одного атома до другого. Для простоты мы будем писать ( q / ℏ ) A x ≡ f ( x ), поскольку А х , вообще говоря, зависит от х . Если обозначить через С ( х )≡ С n амплитуду того, что электрон обнаружится возле атома n , расположенного в точке х , то скорость изменения этой амплитуды будет даваться уравнением

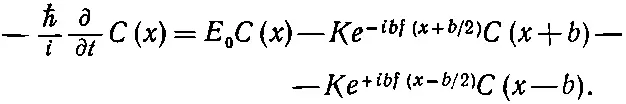(19.4)

В нем три части. Во-первых, у электрона, который находится в точке х , есть некоторая энергия Е 0. Это, как обычно, дает член Е 0 С ( х ). Затем имеется член — КС ( х + b ), т. е. амплитуда того, что электрон от атома n +1, расположенного в х + b , отпрыгнул на шаг назад. Однако если это происходит в присутствии векторного потенциала, то фаза амплитуды обязана сместиться согласно правилу (19.1). Если А х на расстоянии между соседними атомами заметно не изменяется, то интеграл можно записать попросту в виде значения А х посредине, умноженного на расстояние. Итак, произведение ( iq / ℏ ) на интеграл равно ibf ( x + b /2). А раз электрон прыгал назад, я этот сдвиг фазы отмечаю знаком минус. Это дает вторую часть. И точно так же имеется некоторая амплитуда того, что будет прыжок вперед, но на этот раз уже берется векторный потенциал с другой стороны от х , на расстоянии b /2, и умножается на расстояние b . Это дает третью часть. В сумме получается уравнение для амплитуды того, что частица в поле, характеризуемом векторным потенциалом, окажется в точке х .

Но дальше мы знаем, что если функция С ( х ) достаточно плавная (мы берем длинноволновый предел) и если мы сдвинем атомы потеснее, то уравнение (14.4) будет приблизительно описывать поведение электрона в пустоте. Поэтому следующим шагом явится разложение обеих сторон (19.4) по степеням b , считая b очень малым. К примеру, если b =0, то правая часть будет равна просто ( Е 0-2 К ) С ( х ), так что в нулевом приближении энергия равняется Е 0-2 К . Затем пойдут степени b , но из-за того, что знаки показателей экспонент противоположны, останутся только четные степени. В итоге, если вы разложите в ряд Тэйлора С ( х ), f ( x ) и экспоненты и соберете затем члены с b 2, вы получите

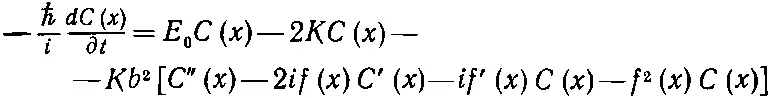(19.5)

(штрихи обозначают дифференцирование по х ).

Это ужасное нагромождение разных букв выглядит очень сложно. Но математически оно в точности совпадает с

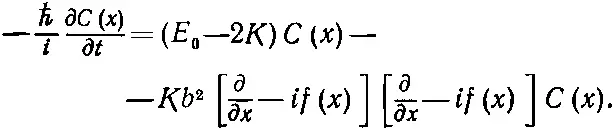(19.6)

Вторая скобка, действуя на С ( х ), даст С '( х ) минус if ( x ) C ( x ). Первая скобка, действуя на эти два члена, даст член с С ", члены с первыми производными f ( x ) и с первой производной С ( х ). А теперь вспомните, что решения в нулевом магнитном поле (см. гл. 11, §3) изображают частицу с эффективной массой m эфф, даваемой формулой

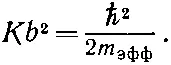
Если вы затем положите Е 0=+2 К и снова вернетесь к f ( x )=( q / ℏ ) A x , то легко убедитесь, что (19.6) это то же самое, что первая часть (19.3). (Происхождение члена с потенциальной энергией хорошо известно, и я не буду им заниматься.) Утверждение (19.1) о том, что векторный потенциал умножает все амплитуды на экспоненциальный множитель, равнозначно правилу, что оператор импульса (ℏ/ i )∇ заменяется на (ℏ/ i )∇- q A, как мы и сделали в уравнении Шредингера (19.3).