Ричард Фейнман - Том 3. Квантовая механика

Одна из забавных сторон манипуляций с операторами заключается в том, что многие классические уравнения переносятся в квантовомеханическую форму. А какие нет? Ведь должны же быть такие, которые не получаются, потому что если бы все повторялось, то в квантовой механике не было бы ничего отличного от классической, не было бы новой физики.

Вот вам уравнение, которое отличается. В классической физике

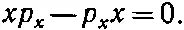
А что в квантовой механике?

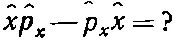
Подсчитаем это в x -представлении. Чтобы было видно, что мы делаем, приложим это к некоторой волновой функции ψ( x ). Пишем

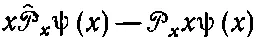
или

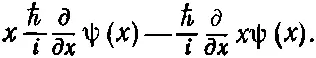
Вспомним теперь, что производные действуют на всё, что справа. Получаем

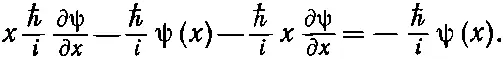(18.73)

Ответ не нуль. Вся операция попросту равнозначна умножению на -ℏ/ i :

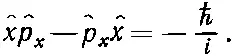(18.74)

Если бы постоянная Планка была равна нулю, то квантовые и классические результаты стали бы одинаковыми и не пришлось бы нам учить никакой квантовой механики!

Отметим, что если два каких-то оператора А и В , взятые в сочетании

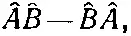
не дают нуля, то мы говорим, что «операторы не перестановочны», или «операторы не коммутируют». А уравнение наподобие (18.74) называется «перестановочным соотношением». Вы можете сами убедиться, что перестановочное соотношение для p х и у (или коммутатор р х и у ) имеет вид

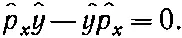
Существует еще одно очень важное перестановочное соотношение. Оно относится к моментам количества движения. Вид его таков:

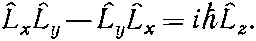(18.75)

Если вы хотите приобрести некоторый опыт работы с операторами ^ x и ^ p , попробуйте доказать эту формулу сами.

Интересно заметить, что операторы, которые не коммутируют, можно встретить и в классической физике. Мы с этим уже сталкивались, когда говорили о поворотах в пространстве. Если вы повернете что-нибудь, например книжку, сперва на 90° вокруг оси х , а затем на 90° вокруг оси у , то получится совсем не то, что было бы, если бы сначала вы повернули ее на 90° вокруг оси у , а после на 90° вокруг оси х . Именно это свойство пространства и ответственно за уравнение (18.75).

Теперь мы познакомим вас с еще одной интересной вещью: вы узнаете, как средние изменяются во времени. Представим на минуту, что у нас есть оператор ^ A , в который время явным образом не входит. Имеется в виду такой оператор, как ^ x или ^ p . [А исключаются, скажем, такие вещи, как оператор внешнего потенциала V ( x, t ), меняющийся во времени.] Теперь представим, что мы вычислили < A > срв некотором состоянии |ψ>, т. е.

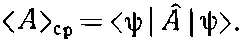(18.76)

Как < A > србудет зависеть от времени? Но почему оно вообще может зависеть от времени? Ну, во-первых, может случиться, что оператор сам явно зависит от времени, например, если он был связан с переменным потенциалом типа V ( x, t ). Но даже если оператор от t не зависит, например оператор ^ A =^ x , то соответствующее среднее может зависеть от времени. Ведь среднее положение частицы может перемещаться. Но как может такое движение получиться из (18.76), если А от времени не зависит? Дело в том, что во времени может меняться само состояние |ψ>. Для нестационарных состояний мы часто даже явно отмечали зависимость от времени, записывая их как |ψ( t )>. Теперь мы хотим показать, что скорость изменения < A > срдается новым оператором, который мы обозначим ^A. Напомним, что ^A это оператор, так что точка над А вовсе не означает дифференцирования по времени, а является просто способом записи нового оператора ^A, определяемого равенством

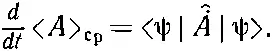(18.77)

Задачей нашей будет найти оператор ^ .A.

Прежде всего, нам известно, что скорость изменения состояния дается гамильтонианом. В частности,

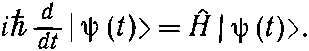(18.78)

Это всего-навсего абстрактная форма записи нашего первоначального определения гамильтониана

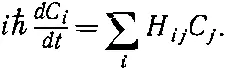(18.79)

Если мы комплексно сопряжем это уравнение, оно будет эквивалентно

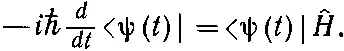(18.80)

Посмотрим теперь, что случится, если мы продифференцируем (18.76) по t . Поскольку каждое ψ зависит от t , мы имеем

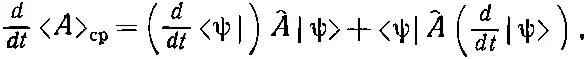(18.81)

Наконец, заменяя производные ихвыражениями (18.78) и (18.80), получаем

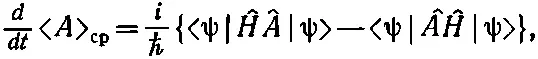
а это то же самое, что написать

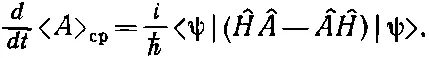
Сравнивая это уравнение с (18.77), мы видим, что

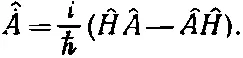(18.82)

Это и есть то интересное соотношение, которое мы обещали; и оно справедливо для любого оператора А .

Кстати заметим, что, если бы оператор А сам зависел от времени, мы бы получили