Ричард Фейнман - Том 3. Квантовая механика

Ну что ж, начнем раскладывать (18.48) в x -представлении.

Напишем

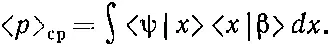(18.52)

Но теперь надо знать другое: как выглядит состояние |β> в x -представлении. Если мы узнаем это, мы сможем взять интеграл. Итак, наша задача — найти функцию β( x )=< x |β>. Ее можно найти следующим образом. Мы видели в гл. 14, § 3, как < р |β> связано с < x |β>. Согласно уравнению (14.24),

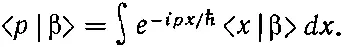(18.53)

Если нам известно < р |β>, то, решив это уравнение, мы найдем < x |β>. Но результат, конечно, следовало бы как-то выразить через ψ( x )=< x |ψ>, потому что считается, что именно эта величина нам известна. Будем теперь исходить из (18.47) и, опять применив (14.24), напишем

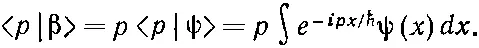(18.54)

Интеграл берется по х , поэтому р можно внести под интеграл

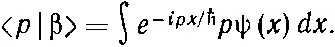(18.55)

Теперь сравним это с (18.53). Может быть, вы подумали, что < x |β> равно p ψ( x )? Нет, напрасно! Волновая функция < х |β>=β( x ) может зависеть только от х , но не от р . В этом-то вся трудность.

К счастью, кто-то заметил, что интеграл в (18.55) можно проинтегрировать по частям. Производная e - ipx / ℏ по х равна (- i / ℏ ) pe - ipx / ℏ , поэтому интеграл (18.55) это все равно, что

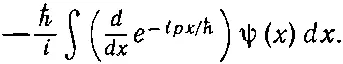
Если это проинтегрировать по частям, оно превратится в

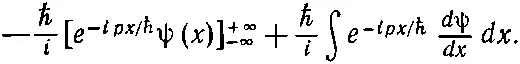
Пока речь идет только о связанных состояниях, ψ( x ) стремится к нулю при х →±∞, скобка равна нулю и мы имеем

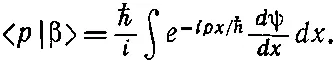(18.56)

А вот теперь сравним этот результат с (18.53). Вы видите, что

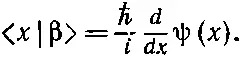(18.57)

Все необходимое, чтобы взять интеграл в (18.52), у нас уже есть. Окончательный ответ таков:

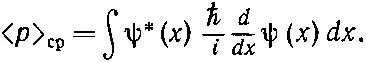(18.58)

Мы узнали, как выглядит (18.48) в координатном представлении. Перед нами начинает постепенно вырисовываться интересная картина. Когда мы задали вопрос о средней энергии состояния |ψ>, то ответ был таков:

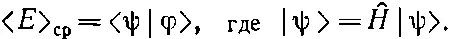
То же самое в координатном мире записывается так:

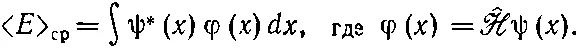
Здесь ^ℋ — алгебраический оператор, который действует на функцию от х .

Когда мы задали вопрос о среднем значении х , то тоже обнаружили, что ответ имеет вид

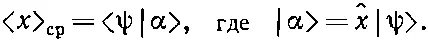
В координатном мире соответствующие уравнения таковы:

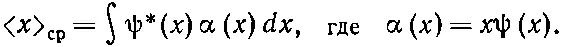
Когда мы задали вопрос о среднем значении р , то ответ оказался

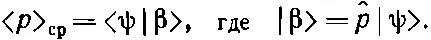
В координатном мире эквивалентные уравнения имели бы вид

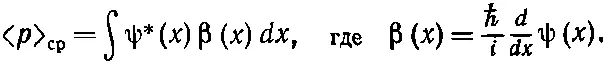
Во всех наших трех примерах мы исходили из состояния |ψ> и создавали новое (гипотетическое) состояние с помощью квантовомеханического оператора. В координатном представлении мы генерируем соответствующую волновую функцию, действуя на волновую функцию ψ( x ) алгебраическим оператором. Можно говорить о взаимнооднозначном соответствии (для одномерных задач) между

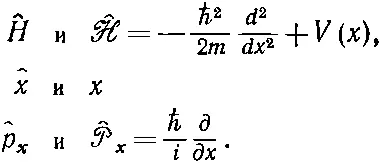(18.59)

В этом перечне мы ввели новый символ ^℘ xдля алгебраического оператора (ℏ/ i )∂/∂ x :

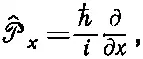(18.60)

и поставили под ^℘ значок х , чтобы напомнить, что имеем пока дело с одной только x -компонентой импульса.

Результат этот легко обобщается на три измерения. Для других компонент импульса

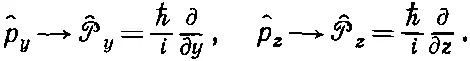
При желании можно даже говорить об операторе вектора импульса и писать

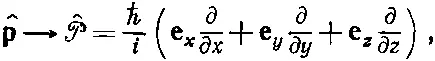
где е х , е y и е z — единичные векторы в трех направлениях. Можно записать это и еще изящнее:

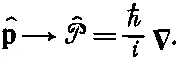(18.61)

Окончательный вывод наш таков: по крайней мере для некоторых квантовомеханических операторов существуют соответствующие им алгебраические операторы в координатном представлении. Все, что мы до сих пор вывели (с учетом трехмерности мира), подытожено в табл. 18.1.

Таблица 18.1. АЛГЕБРАИЧЕСКИЕ ОПЕРАТОРЫ В КООРДИНАТНОМ ПРЕДСТАВЛЕНИИ

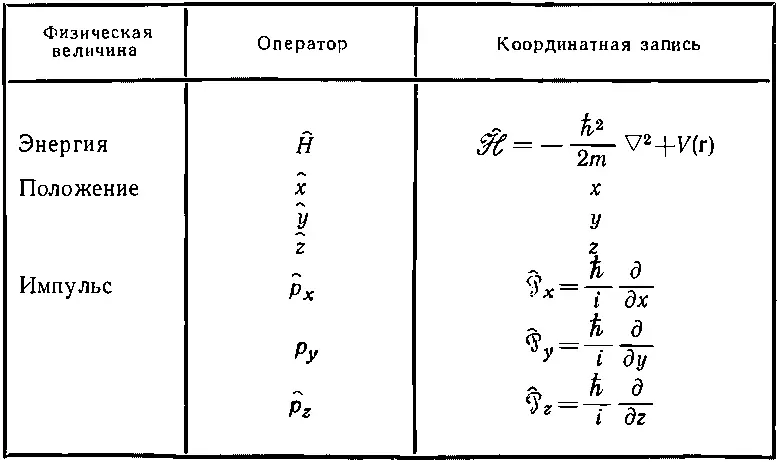
Каждый оператор может быть представлен в двух равноценных видах [86] Во многих книжках для ^ A и ^ A [ script ] используется один и тот же символ: физика в них одна и та же, да и удобнее все время обходиться без новых букв. А из контекста всегда ясно, что имеется в виду. :

либо

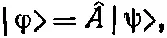(18.62)

либо

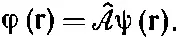(18.63)