Ричард Фейнман - Том 3. Квантовая механика

Величина в фигурных скобках в (18.27) это алгебраический оператор. [«Оператор» V ( x ) означает «умножь на V ( x )».] Мы обозначим его ^ℋ

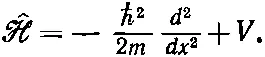
В этих обозначениях (18.23) превращается в

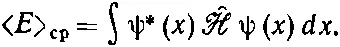(18.28)

Определенный здесь алгебраический оператор ^ℋ, конечно, не тождествен с квантовомеханическим оператором ^ H . Новый оператор действует на функцию координаты ψ( x )=< x |ψ>, образуя новую функцию от х , φ( x )=< x |φ>, а ^ H действует на вектор состояния |ψ>, образуя другой вектор состояния |ф>, причем не имеется в виду ни координатное, ни вообще какое-либо частное представление. Мало того, даже в координатном представлении ^ℋ не совсем то же, что ^ H . Если бы мы решили работать в координатном представлении, то смысл оператору ^ H пришлось бы придавать с помощью матрицы < x |^ H | x '>, которая как-то зависит от двух «индексов» x и x '; иначе говоря, следовало бы ожидать, что [как утверждает (18.25)] < x |φ> связано со всеми амплитудами < x |ψ> операцией интегрирования. А с другой стороны, мы нашли, что ^ℋ — это дифференциальный оператор. Связь между < x |^ H | х '> и алгебраическим оператором ^ℋ мы уже выясняли в гл. 14, § 5.

Наши результаты нуждаются в одном уточнении. Мы предположили, что амплитуда ψ( x )=< x |ψ> нормирована, т. е. масштабы выбраны так, что

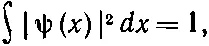
и вероятность увидеть электрон все равно где равна единице. Но вы могли бы, если бы захотели работать с ненормированной ψ( х ), следовало бы только писать

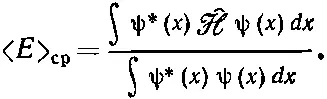(18.29)

Это одно и то же.

Обратите внимание на сходство между (18.28) и (18.18). Оба эти способа записи одного и того же результата при работе в x -представлении часто встречаются. От первого можно перейти ко второму, если ^ A — локальный оператор, т. е. такой, для которого интеграл

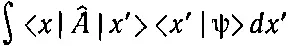
может быть записан в виде ^ A [ script ]ψ( x ), где ^ A [ script ]— дифференциальный алгебраический оператор. Однако встречаются операторы, для которых это неверно. Тогда приходится работать с исходными уравнениями (18.21) и (18.22).

Наш вывод легко обобщается на три измерения. Итог таков [83] Элемент объема мы обозначаем dОбъем . Он попросту равен dxdydz , а интеграл берется от -∞ до +∞ по всем трем координатам. :

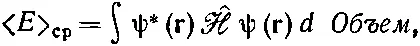(18.30)

где

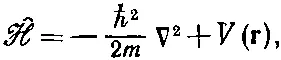(18.31)

причем подразумевается, что

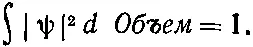(18.32)

Такие же уравнения получаются довольно очевидным образом и при обобщении на системы с несколькими электронами, но мы не будем сейчас заниматься выписыванием результатов.

С помощью (18.30) можно рассчитать среднюю энергию атомного состояния, даже не зная уровней энергии. Нужна только волновая функция. Это очень важный закон. Расскажем об одном интересном его применении. Пусть вам нужно узнать энергию основного состояния некоторой системы, скажем атома гелия, но вы затрудняетесь решить уравнение Шредингера для волновой функции из-за большого числа переменных. Положим, однако, что вы решили попробовать какую-то волновую функцию (выбрав ее по своему желанию) и подсчитать среднюю энергию. Иначе говоря, вы пользуетесь уравнением (18.29), обобщенным на три измерения, чтобы узнать, какова была бы средняя энергия, если бы атом был на самом деле в состоянии, описываемом этой волновой функцией. Эта энергия, бесспорно, окажется выше энергии основного состояния — самой низкой энергии, какую может иметь атом [84] Можно выразить это и иначе. Какую бы функцию (т. е. состояние) вы ни выбрали, ее всегда можно представить в виде линейной комбинации базисных состояний, являющихся состояниями с определенной энергией. Поскольку в этой комбинации присутствует примесь состояний с более высокими энергиями, то средняя энергия окажется выше энергии основного состояния. . Возьмем теперь новую функцию и вычислим новую среднюю энергию. Если она ниже, чем было при первом вашем выборе, значит, вы подошли ближе к истинной энергии основного состояния. Если вы немного поразмыслите, вы, конечно, начнете пробовать такие функции, в которых есть несколько свободных параметров. Тогда энергия выразится через эти параметры. Варьируя параметры так, чтобы получить наинизшую мыслимую энергию, вы тем самым перепробуете за один раз целый класс функций. Скорее всего вы обнаружите, что понижать энергию становится все труднее и труднее, т. е. начнете убеждаться в том, что уже довольно близко подошли к наинизшей возможной энергии. Именно так и был решен атом гелия — никаких дифференциальных уравнений не решали, а составили особые функции со множеством поддающихся подгонке параметров, которые были подобраны так, чтобы дать средней энергии наинизшее значение.

Каково среднее местоположение электрона в атоме? В данном состоянии |ψ> каково среднее значение координаты х ? Разберем одномерный случай, а обобщение на трехмерный или на системы с большим числом частиц останется на вашу долю. Мы имеем состояние, описываемое функцией ψ( x ), и продолжаем раз за разом измерять х . Что получится в среднем? Очевидно, ∫ xP ( x ) dx , где Р ( х )—вероятность обнаружить электрон в небольшом элементе длины dx возле х . Пусть плотность вероятности Р ( х ) меняется с х так, как показано на фиг. 18.1.

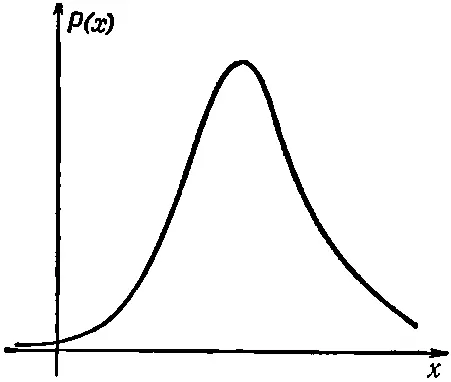
Фиг. 18.1. Кривая плотности вероятности, представляющей локализованную частицу.

Вероятнее всего вы обнаружите электрон где-то возле вершины кривой. Среднее значение х тоже придется куда-то на область невдалеке от вершины, а точнее, как раз на центр тяжести площади, ограниченной кривой.