Ричард Фейнман - Том 3. Квантовая механика

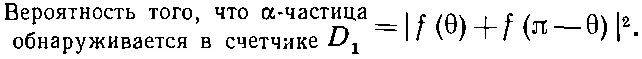(1.15)

Это совсем не то, что (1.14). Возьмите, скажем, угол π/2 (это легче себе представить). При θ=π/2 мы, естественно, имеем f (θ)=f(π-θ), так что из (1.15) вероятность оказывается равной

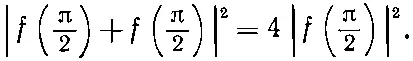
А с другой стороны, если бы не было интерференции, формула (1.14) дала бы только 2| f (π/2)| 2. Так что на угол 90° рассеивается вдвое больше частиц, чем можно было ожидать. Конечно, и под другими углами результаты будут другие. И мы приходим к необычному выводу: когда частицы тождественны, происходит нечто новое, чего не бывало, когда частицы можно было друг от друга отличить. При математическом описании вы обязаны складывать амплитуды взаимоисключающих процессов, в которых обе частицы просто обмениваются ролями, и происходит интерференция.

Еще более неожиданное явление происходит с рассеянием электронов на электронах или протонов на протонах. Тогда не верен ни один из прежних результатов! Для этих частиц мы должны призвать на помощь совершенно новое правило: если попадающий в некоторую точку электрон обменивается своей индивидуальностью с другим электроном, то новая амплитуда интерферирует со старой в противофазе . Это все равно интерференция, но с обратным знаком. В случае α-частиц, когда происходит обмен α-частицами, достигающими счетчика, амплитуды интерферируют с одним и тем же знаком. А в случае электронов амплитуды обмена интерферируют с разными знаками . С точностью до одной детали, о которой будет сейчас сказано, правильная формула для электронов в опыте, подобном изображенному на фиг. 1.8, такова:

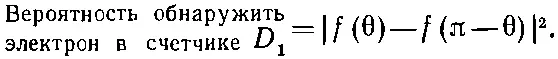(1.16)

Это утверждение нуждается в уточнении, потому что мы не учли спин электрона (у α-частиц спина нет).

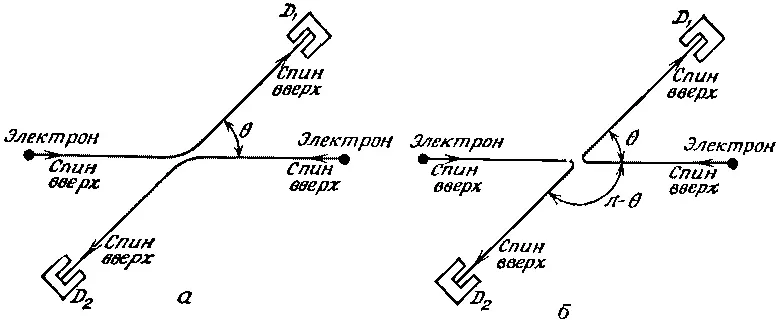
Фиг. 1.8. Рассеяние электронов на электронах. Если спины сталкивающихся электронов параллельны, то процессы а и б неразличимы.

Спин электрона можно считать направленным либо вверх, либо вниз по отношению к плоскости рассеяния. Если энергия в опыте достаточно низка, то магнитные силы, возникающие от токов, будут малы и не повлияют на спин. Предположим в нашем анализе, что так оно и есть, так что нет шансов, чтобы спины при столкновении перевернулись. Какой бы спин у электрона ни был, он уносит его с собой. Мы видим теперь, что есть много возможностей. У частицы-снаряда и частицы-мишени оба спина могут быть направлены вверх, или вниз, или в разные стороны. Если они оба направлены вверх, как на фиг. 1.8 (или оба — вниз), то после рассеяния останется то же самое, и амплитуда процесса будет разностью амплитуд тех двух возможностей, которые показаны на фиг. 1.8. Вероятность обнаружить электрон в счетчике D 1тогда будет даваться формулой (1.16).

Предположим, однако, что у «снаряда» спин направлен вверх, а у «мишени» — вниз. У электрона, попавшего в счетчик D 1, спин может оказаться либо направленным вверх, либо —вниз, и, измеряя этот спин, мы можем сказать, выскочил ли этот электрон из бомбардирующего пучка или же из мишени.

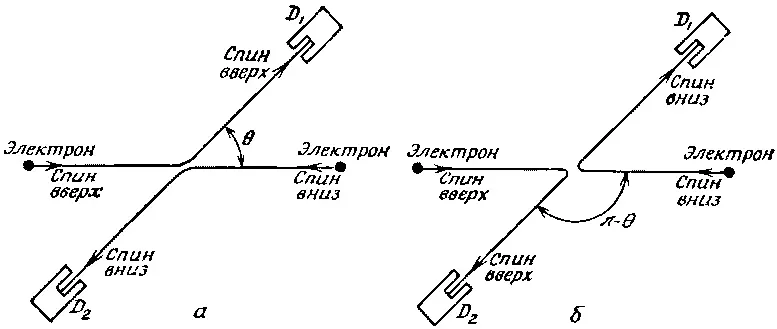
Фиг. 1.9. Рассеяние электронов с антипараллельными спинами.

Эти две возможности показаны на фиг. 1.9; в принципе они различимы, и поэтому интерференции не получится, просто сложатся две вероятности. Все это верно и тогда, когда оба первоначальных спина перевернуты, т. е. если спин слева смотрит вниз, а спин справа — вверх.

Таблица 1.1. РАССЕЯНИЕ НЕПОЛЯРИЗОВАННЫХ ЧАСТИЦ СО СПИНОМ 1/ 2

Наконец, если электроны вылетают случайно (например, они вылетают из накаленной вольфрамовой нити полностью неполяризованным пучком), то с равной вероятностью каждый отдельный электрон вылетит либо спином вверх, либо спином вниз. Если мы не собираемся в нашем опыте измерять в какой-нибудь точке спин электронов, то получается то, что называют экспериментом с неполяризованными частицами. Результат этого эксперимента лучше всего подсчитать, перечислив все мыслимые возможности, как это сделано в табл. 1.1. Для каждой различимой альтернативы отдельно подсчитана вероятность . Тогда полная вероятность есть сумма всех отдельных вероятностей. Заметьте, что для неполяризованных пучков результат при θ=π/2 составляет половину классического результата для независимых частиц.

Поведение тождественных частиц приводит ко многим интересным следствиям; в следующей главе мы обсудим их поподробнее.

Повторить : гл. 41 (вып. 4) «Броуновское движение» (об излучении абсолютно черного тела); гл. 42 (вып 4) «Применения кинетической теории»

В предыдущей главе мы начали рассматривать особые правила, по которым происходит с интерференция в процессах с двумя тождественными частицами. Тождественными мы считаем такие частицы, которые, подобно электронам, никак невозможно отличить друг от друга. Если в процессе имеются две тождественные частицы, то замена той, которая повернула к счетчику, на другую — это неотличаемая альтернатива, которая, как и во всех случаях неотличимых альтернатив, интерферирует с первоначальным случаем, когда обмена не было. Амплитудой события тогда служит сумма двух интерферирующих амплитуд, и существенно, что в одних случаях интерференция происходит в фазе , а в других — в противофазе .

Представим, что сталкиваются две частицы а и b и частица а рассеивается в направлении 1, а частица b — в направлении 2 (фиг. 2.1, а).

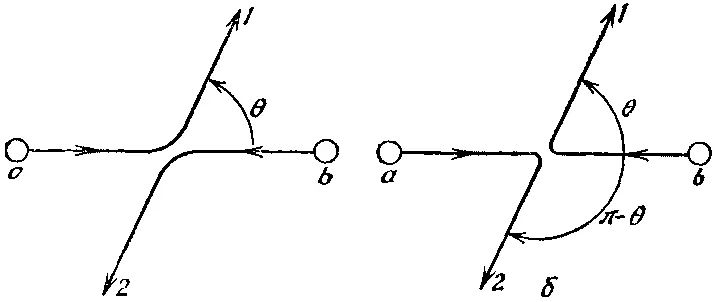
Фиг. 2.1. При рассеянии двух тождественных частиц процессы а и б неразличимы.

Пусть f (θ) будет амплитуда этого процесса; тогда вероятность Р 1наблюдения подобного события пропорциональна | f (θ)| 2. Конечно, могло случиться, что частица b рассеялась в счетчик 1, а частица а направилась в счетчик 2 (фиг. 2.1, б ). Если считать, что никаких специальных направлений, определяемых спином или чем-то подобным, в опыте нет, то вероятность Р 2этого события можно просто записать в виде | f (π-θ)| 2, потому что этот процесс попросту эквивалентен первому процессу, в котором счетчик 1 поставили под углом (π-θ). И вам могло бы показаться, что амплитуда второго процесса равна просто f (π-θ). Но это не обязательно так, потому что в ней мог стоять произвольный фазовый множитель. Иначе говоря, амплитуда могла бы быть такой: