Йэн Стюарт - Математика космоса [Как современная наука расшифровывает Вселенную]

В 1924 году Артур Эддингтон показал, что сингулярность Шварцшильда — не физическое явление, а математический артефакт. Математики представляют искривленные пространства и пространство-время при помощи сетки кривых или поверхностей, помеченных числами и напоминающих линии широты и долготы на карте Земли. Такие сетки называются координатными системами. Эддингтон показал, что сингулярность Шварцшильда — это особенность выбранной им системы координат, подобно тому, как на Северном полюсе Земли меридианы сходятся, а параллели образуют все более мелкие круги. Однако если вы стоите на Северном полюсе, то земная поверхность там геометрически выглядит точно так же, как в других местах. Только снега и льда больше. Внешние странности геометрии возле Северного полюса вызваны тем, что в качестве координат выбраны широта и долгота. Если бы вы воспользовались системой координат с Восточным и Западным полюсами на экваторе, то уже эти точки выглядели бы странно, а Северный и Южный полюса казались совершенно нормальными местами.

Координаты Шварцшильда корректно представляют, как выглядит черная дыра снаружи, но изнутри она смотрится совершенно иначе. Эддингтон нашел другую систему координат, при которой сингулярность Шварцшильда исчезает. К несчастью, он не смог исследовать свое открытие до конца, поскольку работал в то время над другими астрономическими вопросами, — и открытие осталось почти незамеченным. Интерес к нему вновь пробудился в 1933 году, когда Жорж Леметр независимо от Эддингтона понял, что сингулярность в решении Шварцшильда — математический артефакт.

Но даже после этого тема лишь теплилась до 1958 года, когда Дэвид Финкельштейн нашел новую более удобную координатную систему, в которой радиус Шварцшильда имеет физический смысл, но смысл этот не в том, что время там замирает. При помощи своих координат Финкельштейн решил уравнения поля не только для внешнего наблюдателя, но и для всего будущего, которое ожидает внутреннего наблюдателя. В этих координатах на радиусе Шварцшильда нет никакой сингулярности, но радиус этот представляет собой горизонт событий : односторонний барьер, для которого внешняя часть может влиять на внутреннюю, но не наоборот. Его решение демонстрирует, что звезда, лежащая полностью внутри своего радиуса Шварцшильда, коллапсирует и образует область, покинуть которую не может ни вещество, ни даже фотоны. Такая область оказывается частично оторванной от остальной Вселенной — в нее можно попасть, но из нее невозможно выйти. Это и есть настоящая черная дыра в современном понимании этого термина.

Как выглядит черная дыра, зависит от наблюдателя. Представьте себе, что некий неудачливый космический корабль — ну, или космический корабль с неудачливым экипажем — падает в черную дыру. Это один из столпов, на которых зиждется научно-фантастическое кино, но мало кому из кинематографистов удается снять этот процесс хоть сколько-нибудь правдоподобно. В фильме «Интерстеллар» это удалось сделать благодаря тому, что консультантом выступил Кип Торн, но у сюжета этого фильма есть свои недостатки. По данным физики, если мы наблюдаем за падающим кораблем издалека, то он, как нам кажется, падает все медленнее и медленнее, потому что гравитация черной дыры все сильнее притягивает фотоны, идущие от корабля. Те фотоны, что оказываются к черной дыре достаточно близко, не могут уйти вовсе; те, что оказались непосредственно за горизонтом событий с внешней стороны, где сила тяжести в точности компенсирует скорость света, могут уйти, но очень медленно. Мы видим космический корабль благодаря тому, что регистрируем испускаемый им свет, поэтому мы видим, что он ползет все медленнее и в конце концов останавливается, не доходя до горизонта событий. Общая теория относительности гласит, что гравитация замедляет время. На радиусе Шварцшильда время останавливается , но только с точки зрения внешнего наблюдателя. Более того, сама дыра становится все краснее и краснее благодаря эффекту Доплера. Вот почему черные дыры, независимо от штампованного сарказма Холли, на самом деле не черные.

Экипаж космического корабля не испытывает ничего подобного. Астронавты приближаются к черной дыре, их засасывает внутрь через горизонт событий, а затем…

…Они испытывают на себе решение уравнения, с точки зрения наблюдателя, внутри черной дыры. Вероятно. Мы не знаем наверняка, потому что, судя по уравнениям, все вещество в корабле будет сжато в математическую точку бесконечной плотности и нулевого размера. Это, если так действительно произойдет, и будет настоящая физическая сингулярность, не говоря уже о фатальности такого развития событий.

Специалисты по математической физике не слишком любят говорить о сингулярностях. Как правило, если где-то вдруг объявляется сингулярность, это значит, что математическая модель теряет связь с реальностью. В данном случае мы не можем направить зонд в черную дыру и вывести его потом обратно или хотя бы принять с него радиосигналы (которые путешествуют со скоростью света и тоже не могут оттуда выйти), так что у нас нет никакой возможности выяснить, в чем состоит реальность. Однако представляется вероятным, что любое развитие событий, каким бы оно ни было, окажется неприятно жестким, и экипаж его не переживет. Конечно, если это не кино. По крайней мере некоторым экипажам в некоторых фильмах это по силам.

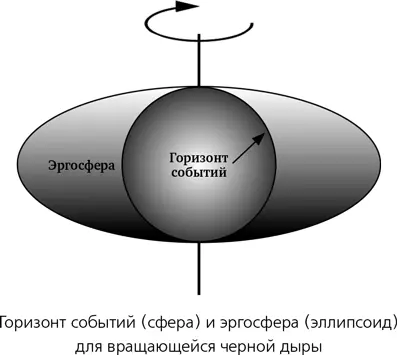
Математика черных дыр — дело тонкое, и первоначально единственным типом черной дыры, для которого уравнения поля можно было решить в явном виде, была черная дыра по Финкельштейну, то есть черная дыра, которая не вращается и не имеет электрического поля. Черные дыры такого типа часто называют шварцшильдовскими. Надо сказать, то специалист по математической физике Мартин Крускал нашел аналогичное решение даже раньше, но не опубликовал его. На его основе Крускал и Дьордь Секереш разработали то, что сегодня называется координатами Крускала — Секереша и описывает внутренность черной дыры более детально. Основная геометрия очень проста: сферический горизонт событий с точечной сингулярностью в центре. Все, что падает в черную дыру, достигает точки сингулярности за конечный промежуток времени.

Черная дыра такого рода — особый случай, поскольку в большинстве своем небесные тела вращаются. Когда коллапсирует вращающаяся звезда, получившаяся на ее месте черная дыра тоже будет вращаться по закону сохранения момента импульса. В 1963 году Рой Керр вытащил из шляпы математического кролика, записав метрику пространства-времени для вращающейся черной дыры — метрику Керра. Поскольку уравнения поля нелинейны, наличие точной формулы примечательно само по себе. Она показывает, что вместо единственного сферического горизонта событий там существуют две критические поверхности, на которых физические свойства резко меняются. Внутренняя из этих поверхностей — это сферический горизонт событий; как и в случае статичной черной дыры, он представляет собой барьер, который свет не в состоянии преодолеть. Внешняя поверхность — это уплощенный эллипсоид, на полюсах касающийся горизонта событий.