Йэн Стюарт - Математика космоса [Как современная наука расшифровывает Вселенную]

Область между двумя этими поверхностями называется эргосферой. «Эргон» по-гречески означает «работа», и название объясняется тем, что из черной дыры, используя ее эргосферу, можно извлекать энергию. Если некая частица падает внутрь эргосферы, то релятивистский эффект, известный как увлечение инерциальных систем отсчета, заставляет ее начать вращение вместе с черной дырой, что увеличивает ее энергию. Но поскольку частица при этом по-прежнему находится за пределами горизонта событий, она может — при определенных обстоятельствах — уйти от нее и унести эту энергию с собой. Таким образом, частица извлекает из черной дыры энергию, то есть делает то, что невозможно проделать со статичной черной дырой.

Помимо вращения, черная дыра может обладать электрическим зарядом. Ганс Рейсснер и Гуннар Нордстрём нашли метрику для заряженной черной дыры — метрику Рейсснера — Нордстрёма. В 1965 году Эзра Ньюмен открыл метрику для осесимметричной вращающейся заряженной черной дыры — метрику Керра — Ньюмена. Казалось бы, могут существовать и более сложные типы черных дыр, но физики считают, что это не так, за исключением разве что магнитной дыры. Гипотеза о лысой черной дыре гласит, что после того, как формирование черной дыры завершилось, у нее остается лишь три базовых физические свойства: масса, спин и заряд. Название гипотезы происходит от фразы «У черных дыр нет волос» в книге 1973 года «Гравитация», написанной Чарльзом Мизнером, Кипом Торном и Джоном Уилером и ставшей настоящей библией по этому вопросу. Уилер приписывает эту фразу Яакову Бекенштейну.

Это утверждение часто называют теоремой о лысой черной дыре, но на самом деле оно пока не доказано, а именно это, как правило, подразумевает слово «теорема». Опровергнуто оно, естественно, тоже не было. Стивен Хокинг, Брэндон Картер и Дэвид Робинсон сумели доказать некоторые особые случаи. Если, как считают некоторые физики, черная дыра может обладать и магнитным полем тоже, гипотезу придется модифицировать, чтобы она включала в себя и эту возможность.

Давайте познакомимся немного с геометрией черной дыры и попробуем получить представление о том, насколько странны эти структуры.

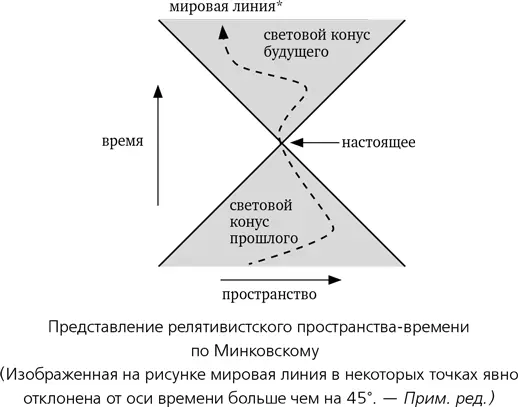
В 1907 году Герман Минковский придумал простую геометрическую картинку релятивистского пространства-времени. Я воспользуюсь упрощенным изображением всего с одним пространственным измерением и обычным измерением времени, но в принципе его можно распространить и на физически реалистичную картину с тремя пространственными измерениями. В этом представлении изогнутые «мировые линии» отражают движение частиц. По мере изменения временной координаты результирующую пространственную координату можно считать с этой кривой. Линии, проведенные под углом 45° к осям, представляют частицы, движущиеся со скоростью света. Поэтому мировые линии не могут пересекать никакую линию, направленную под 45°. Точка в пространстве-времени, называемая событием, определяет две такие линии; вместе они образуют его световой конус. Он состоит из двух треугольников: прошлого и будущего. Остальная часть пространства-времени недоступна из этой точки: чтобы попасть туда, вам пришлось бы двигаться быстрее света.

В евклидовой геометрии естественными преобразованиями (координат) являются жесткие перемещения, которые сохраняют расстояния между точками. В специальной теории относительности аналогами этих преобразований являются преобразования Лоренца, а сохраняется при этом величина, называемая интервалом . По теореме Пифагора квадрат расстояния от начала координат до точки на плоскости равен сумме квадратов горизонтальной и вертикальной координат. Квадрат интервала равен квадрату пространственной координаты минус квадрат временной координаты [73] Если принять систему единиц, в которой скорость света равна 1. Тогда время измеряется, скажем, в годах, а пространство — в световых годах. . Эта разница равняется нулю вдоль прямых, проведенных под 45°, и положительна внутри светового конуса. Так что интервал между двумя событиями, которые могут быть связаны причинной связью, представляет собой действительное число. В противном случае это мнимое число, отражающее невозможность движения от одного к другому.

В общей теории относительности в картину включается гравитация; для этого плоскости Минковского позволяют изгибаться, имитируя действие гравитационной силы, как на рисунке в 1 главе.

Пересматривая геометрию Минковского в координатах Крускала — Секереша, Роджер Пенроуз разработал элегантно простой способ изображения релятивистской геометрии черных дыр. Формула метрики явно задает эту геометрию, но на эту формулу можно смотреть до посинения, причем без всякого толку. Но поскольку нам нужна геометрия, может быть, стоит немного порисовать? Картинки не должны противоречить метрике, но хорошая картинка стоит тысячи расчетов.

Диаграммы Пенроуза раскрывают тонкие черты физики черных дыр, позволяя сравнивать различные их типы. Кроме того, эти диаграммы наводят нас на некоторые поразительные, хотя и умозрительные, возможности. Пространство опять упрощается до одного измерения (его располагают горизонтально), время рисуют вертикально, а световые лучи идут под углом 45° и образуют световые конусы, которые разделяют прошлое, будущее и каузально недоступные области.

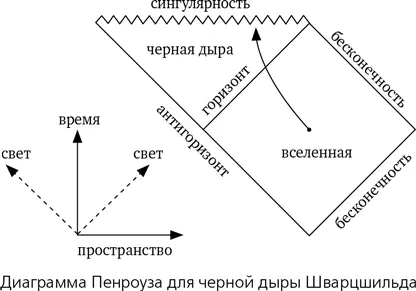
Обычно рисунок Минковского имеет форму квадрата, но в диаграммах Пенроуза вместо этого используется ромб, призванный подчеркнуть особую роль диагональных линий, идущих под 45°. Обе фигуры всего лишь разные способы сжать бесконечную плоскость в конечное пространство. Это необычные, но удобные и полезные системы координат для пространства-времени.

Для разминки начнем с простейшего объекта — черной дыры Шварцшильда. Диаграмма Пенроуза для нее довольно проста. Ромб представляет вселенную [74] Как известно, принято различать нашу Вселенную и другие возможные вселенные. Здесь и в главе 19 обсуждаются различные теоретические варианты вселенных, которые мы будем писать со строчной буквы, даже если они похожи на нашу или сравниваются с ней. — Прим. ред. , в основном соответствующую модели Минковского. Кривая со стрелкой — это мировая линия космического корабля, падающего в черную дыру сквозь ее горизонт (событий) и попадающего в центральную сингулярность (зубчатая линия). Но теперь здесь есть еще и второй горизонт, подписанный «антигоризонт». Это о чем?