Александр Китайгородский - Физика для всех. Книга 3. Электроны

Аккумулятор и батарея являются источниками постоянного тока. А вот электрическая сеть дает нам переменный ток. Слова «постоянный» и «переменный» относятся к величинам напряжения, ЭДС и силы тока. Если в процессе протекания тока все эти величины остаются неизменными, то ток постоянный, если они меняются, то ток переменный.

Характер изменения электрического, тока во времени может быть разным в зависимости от устройства, которое создает ток. Кривую, описывающую изменение электрического тока, можно получить при помощи электронно-лучевой трубки. Электронный луч отклоняется полями двух взаимно перпендикулярных плоских конденсаторов. Накладывая на пластины конденсаторов разные напряжения, можно заставить светящееся пятнышко, оставляемое лучом на экране, бродить по всей плоскости экрана.

Для получения картины переменного тока поступают следующим образом. К одной паре пластин подводят так называемое пилообразное напряжение, кривая которого показана на рис. 4.1.

Если электронный луч находится только под его действием, то пятнышко равномерно движется по экрану, а затем скачком возвращается в исходное положение. Положение пятнышка дает сведения о моменте времени. Если на другую пару пластин наложено изучаемое переменное напряжение, то оно «развернется», совершенно таким же образом, как механическое колебание «разворачивается» с помощью простого устройства, показанного в первой книге.

Сказав «колебание», я не оговорился. Большей частью величины, характеризующие переменный ток, колеблются по тому же гармоническому закону синусоиды, которому подчиняются отклонения маятника от равновесия. Чтобы убедиться в этом, достаточно подключить к осциллографу городской переменный ток.

По вертикали могут быть отложены ток или напряжение. Характеристики тока те же, что и параметры механического колебания. Промежуток времени, после которого картина изменений повторяется, носит, как известно, название периода Т ; частота тока ν — величина, обратная периоду, — равна обычно для городского тока 50 колебаниям в секунду.

Когда рассматривается одна синусоида, то выбор начала отсчета времени безразличен. Если же две синусоиды накладываются друг на друга так, как это показано на рис. 4.2, то надо указать, на какую долю периода они смещены по фазе. Фазой называется угол φ= 2π∙( t/ T). Так что если кривые сдвинуты по отношению друг к другу на четверть периода, то мы говорим, что они смещены по фазе на 90 градусов, если на восьмую часть периода — то значит на 45 градусов по фазе, и т. д.

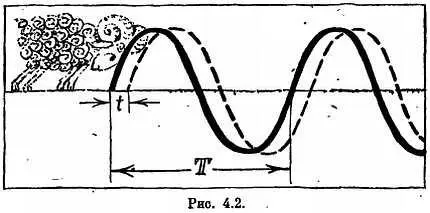
Когда идет речь о нескольких синусоидах, сдвинутых по фазе, техники говорят о векторах тока или напряжения. Длина вектора соответствует амплитуде синусоиды, а угол между векторами — сдвигу фаз. Многие технические устройства дают нам не простой синусоидальный ток, а такой, кривая которого является суммой нескольких смещенных синусоид.

Покажем, что простой синусоидальный ток возникает в том случае, если проводящая рамка вращается в однородном магнитном поле с постоянной скоростью.

При произвольном направлении рамки по отношению к силовым линиям магнитный поток, проходящий через контур, равен

Ф= Ф макс∙sin φ

φ — угол между плоскостью витка и направлением поля.

Этот угол меняется со временем по закону φ= 2π∙( t/ T).

Закон электромагнитной индукции позволяет вычислить ЭДС индукции. Запишем выражения магнитных потоков для двух мгновений, отличающихся на очень малый промежуток времени τ :

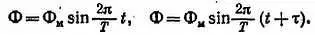
Разность этих выражений:

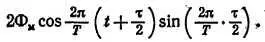
Так как τ очень мало, то справедливы следующие приближенные равенства:

ЭДС индукции равна этой разности, отнесенной ко времени. Значит,

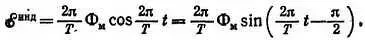
Мы доказали, что ЭДС индукции выражается синусоидой, сдвинутой по отношению к синусоиде магнитного потока на 90 градусов. Что касается максимального значения ЭДС индукции — ее амплитуды, то оно пропорционально произведению амплитуды магнитного потока на частоту вращения рамки.

Закон для силы тока получится, если разделить ЭДС индукции на сопротивление цепи. Но мы сделаем грубую ошибку, если приравняем сопротивление переменному току, которое стоит в знаменателе выражения

I перем= инд/ R перем

омическому сопротивлению — той величине, с которой мы имели дело до сих пор: Оказывается, что R перемопределяется не только омическим сопротивлением, но зависит еще от двух параметров цепи: ее индуктивности и включенных в цепь емкостей.

То, что закон Ома усложняется, когда мы переходим от постоянного тока к переменному, показывает следующий простой опыт. На рис. 4.3 изображена цепь тока, проходящего через электрическую лампочку и катушку, в которую можно вставлять железный сердечник. Сначала подключим лампочку к источнику постоянного тока. Будем вдвигать железный, сердечник в катушку и выдвигать его. Никакого эффекта! Сопротивление цепи не меняется, значит и сила тока остается неизменной.

Но повторим этот же опыт для случая, когда цепь подключена к переменному току. Эффектный результат, не правда ли? Теперь лампочка горит ярко, если сердечник не вставлен в катушку, и тускло, если вы вдвинули железо в катушку.

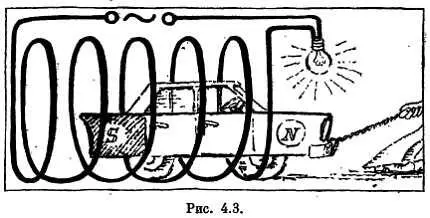
Итак, при неизменном внешнем напряжении, при неизменном омическом сопротивлении (зависящем лишь от материала, длины и сечения проводов) сила тока меняется в зависимости от положения железного сердечника в катушке.

Что это значит?

Мы вспоминаем, что железный сердечник резко увеличивает (в тысячи раз) магнитный поток, проходящий через катушку. В случае переменной ЭДС магнитный поток в катушке все время меняется. Но если без железного сердечника он менялся от нуля до какой-то условной единицы, то при наличии сердечника он будет меняться от нуля до нескольких тысяч единиц.