Александр Китайгородский - Физика для всех. Книга 3. Электроны

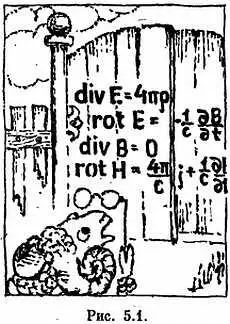
Законы Максвелла указывают нам на то, что не может существовать переменное магнитное поле без электрического и переменное электрическое — без магнитного. Вот по этой причине два прилагательных не разделяют запятой. Электромагнитное поле — это единая сущность.

Отдалившись от зарядов, являющихся источниками электромагнитного поля, мы имеем дело с электромагнитной материей, так сказать, в чистом виде. Не обязательно рассматривать пучки силовых линий. Законы Максвелла могут быть записаны в такой форме, которая применима к точке пространства. Тогда они звучат особенно просто: в точке, в которой меняется во времени электрический вектор, существует и также меняется во времени вектор магнитного поля.

А не есть ли все сказанное чистая фантазия, спросит читатель. Ведь измерение в точке величин быстро меняющихся векторов электрического и магнитного полей — практически не осуществимая задача.

Справедливо! Но о величии законов природы судят по вытекающим из них следствиям. Следствий этих не перечесть. Я нисколько не преувеличу, если скажу, что вся электротехника и радиотехника содержатся в законах Максвелла.

Но об одном важнейшем выводе, вытекающем из уравнений Максвелла, рассказать необходимо. Безупречно строгими вычислениями можно показать, что должно существовать явление электромагнитного излучения.

Пусть в некотором ограниченном участке пространства имеются заряды и токи. В этой системе могут происходить разнообразные энергетические превращения. Механические или химические источники порождают электрические токи, токи в свою очередь могут приводить в движение механизмы и создавать тепло, выделяющееся в проводах. Подсчитаем доходы и убытки. Они не сойдутся! Расчет показывает, что какая-то доля энергии из нашей системы ушла в пространство.

Может ли теория сказать что-либо об этой «излученной» энергии? Оказывается, может. Решение уравнения имеет сложный вид вблизи источника, а вот на расстояниях, существенно превышающих размеры «излучающей» системы, картина становится весьма четкой, а самое главное — проверяемой на опыте.

На больших расстояниях электромагнитное излучение — так мы назовем тот энергетический дефицит, который создается в системе движущихся зарядов, — можно в каждой точке пространства характеризовать направлением распространения. В этом направлении электромагнитная энергия перемещается со скоростью около 300 000 км/с. Эта величина следует из теории!

Второй вывод теории: электрический и магнитный векторы перпендикулярны направлению распространения волны и перпендикулярны друг другу. И, в-третьих, интенсивность электромагнитного излучения (энергия, приходящаяся на единицу площади) падает обратно пропорционально квадрату расстояния.

Поскольку было известно, что свет распространяется как раз со скоростью 300 000 км/с, вычисленной для электромагнитного излучения, и имелись достаточно исчерпывающие сведения о поляризации света, которые заставляли думать, что световая энергия обладает некими «поперечными» свойствами, то Максвелл приходит к заключению: свет является видом электромагнитного излучения.

Лет через десять после кончины Максвелла, в конце восьмидесятых годов, замечательный немецкий физик Генрих Герц (1857–1894) подтвердил на опытах все выводы теории Максвелла. После этих опытов законы Максвелла утвердились на веки вечные в роли одного из считанных по пальцам руки краеугольных камней, на которых покоится здание современного естествознания.

Механические модели противопоставляются математическим. Механические модели можно осуществить при помощи шариков, пружинок, струн, резиновых шнуров и т. д. Механическая модель помогает сделать явление «зримым». Построив механическую модель и продемонстрировав ее действие, мы помогаем человеку попять явление, говоря: вот такая-то величина ведет себя наподобие вот такого-то смещения. Далеко не всякой математической модели можно сопоставить механическую.

Прежде чем говорить 96 электромагнитном излучении, факт которого устанавливается бесчисленным количеством опытов и следует с железной логикой, из уравнений Максвелла, нам нужно побеседовать о возможных механических моделях излучения.

Таких моделей две: корпускулярная и волновая.

Можно изготовить игрушку, которая будет «излучать» во все стороны потоки маленьких частиц — горошинок, маковых зернышек. Это и есть корпускулярная модель, ибо слово «корпускула» значит частица.

Летящая с какой-то скоростью и обладающая некоторой массой частица должна вести себя по законам механики. Частицы способны соударяться, меняя направление своего движения, но обязательно так, чтобы соударение подчинялось законам сохранения энергии и импульса. Какие-то тела могут оказаться непроницаемыми для частиц, и тогда частицы должны, от них отражаться по закону: угол падения равен углу отражения. Частицы могут поглощаться средой. Если в одной среде частицам легче двигаться, чем в другой, то не трудно объяснить явление преломления. Проходя через отверстие в непрозрачном экране, поток частиц, исходящих из точечного источника, должен путешествовать внутри конуса. Правда, возможно незначительное рассеяние, так как небольшая доля частиц может отразиться от краев отверстия. Но, конечно, эти «отражения» могут быть лишь хаотичными и не дадут какого-либо закономерного рисунка, выходящего за пределы геометрической тени.

Волновую модель демонстрируют обычно с помощью водяной ванны. Нетрудно заставить периодически колебаться воду в какой-либо точке. От этой точки, как от камня, брошенного в воду, пойдут круги. Волнообразная поверхность воды видна глазом. Энергия будет распространяться во все стороны, и далеко лежащая щепка придет в колебание с частотой точки, к которой мы подводим энергию.

Звуковые колебания несколько труднее сделать зримыми. Но можно поставить совершенно убедительные эксперименты, которые покажут, что распространение звука — это передача от точки к точке механических смещений среды.

Целый ряд явлений одинаково хорошо объясняются как волновой, так и корпускулярной моделью. Однако обе модели будут одинаково пригодны лишь при дополнительном условии: волна ведет себя так же, как поток частиц, если препятствия и отверстия, которые она встречает на своем пути, много меньше длины волны.

Как мы без труда вычислим по основной формуле, нужной для описания волновой модели, c= ν∙ λ, средней частоте человеческого голоса 1000 Гц соответствует длина волны 30 см. Такая волна будет загибать за угол, если ей придется пройти через метровые отверстия. Но если отверстие имеет размеры порядка сантиметра, то можно говорить о звуковом луче, который проходит сквозь отверстие лишь в том случае, если прямая линия, соединяющая источник и приемник звука, не натыкается на препятствие.