Эрик Роджерс - Физика для любознательных. Том 2. Наука о Земле и Вселенной. Молекулы и энергия

I. Определение массы Солнца и Земли

Ньютон вычислил массу Солнца, выразив ее в земных массах. [В то время масса Земли не была известна и не могла быть определена без измерений, подобных более поздним измерениям, проведенным Кавендишем (см. гл. 23 )

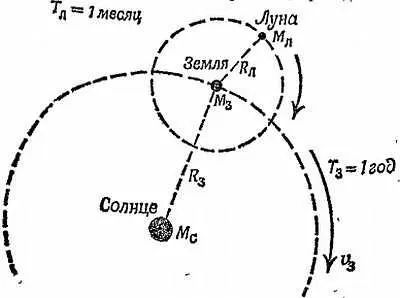
Фиг. 163. Вычисление отношения массы Солнца к массе Земли.

Вычисления могут быть выполнены следующим путем. (Индексы С, 3 и Л относятся к Солнцу, Земле и Луне соответственно.)

Для Движения Земли по орбите вокруг Солнца.

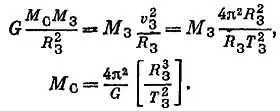
Обратите внимание, что масса Земли М Зсократилась,

Для движения Луны по орбите вокруг Земли:

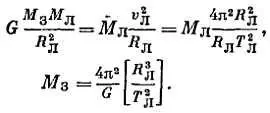
Вновь масса Луны М Лсократилась Теперь, разделив одно уравнение на другое, получим

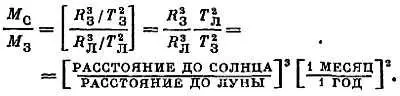
Зная периоды и радиусы орбит, можно вычислить отношение масс Солнца и Земли.

II. Вычисление масс планет

Ньютону удалось оценить массы Юпитера и других планет, у которых есть спутники, в единицах массы Земли или Солнца (Луна не имеет спутников, поэтому ее массу, которая сокращается в первом уравнении, определить нелегко.)

III. Величина g на экваторе

Из-за вращения Земли вокруг своей оси тело будет весить меньше на экваторе, нежели на полюсе, потому что часть его веса должна обеспечить центростремительную силу, удерживающую тело в движении по окружности вместе с поверхностью Земли. Тело, подвешенное на пружинных весах, будет удерживаться меньшей силой, чем сила, действующая на это тело со стороны Земли. Поэтому взвешивание на пружинных весах дает для веса тела меньшее значение, чем его истинный вес, на величину mv 2/ R . Иными словами, напряженность поля силы тяжести Земли будет казаться меньше. Ньютон вычислил эту малую поправку к величине g , которую мы ныне можем наблюдать наряду с влиянием сфероидальной формы Земли.

IV. Несферичность формы Земли

Ньютон рассчитал отклонение формы Земли от сферы, исходя из следующих соображений. Предположим, что Земля вращалась так же, как и теперь, в те времена, когда она представляла собой полужидкую тестообразную массу. Какую форму она должна была принять? Чтобы ответить на этот вопрос, рассмотрим такую схему. Трубка с водой проходит через Северный полюс к центру Земли и оттуда к экватору (фиг. 164). Каков будет уровень воды в трубке у экватора, если трубка заполнена водой так, что-уровень воды у Северного полюса совпадает с поверхностью Земли? Давление воды на дне «полярной» трубки обусловлено весом воды в этой трубке, и это давление передается через колено на дно другого колена трубки. Вес воды во втором колене заставляет воду опускаться. Но в «экваториальной» трубке обе эти силы не равны. Они должны различаться на достаточную величину, чтобы обеспечить направленную внутрь центростремительную силу, действующую на воду в трубке, когда она вращается вместе с Землей вокруг земной оси. Поэтому вес воды в этом колене должен быть больше выталкивающего усилия со стороны «полярной» трубки на величину mv 2/ R , а водяной столб в «экваториальной» трубке должен быть выше, чем в «полярной». «Экваториальная» трубка должна возвышаться над поверхностью Земли, чтобы в ней уместилось дополнительное количество воды. Ньютон вычислил эту дополнительную высоту, оказавшуюся равной 24 км, и пришел к выводу, что на ранней стадии существования Земли, когда она была тестообразной, на — экваторе образовалась выпуклость примерно такой величины. Спустя короткое время измерения размеров Земли подтвердили этот вывод. У Юпитера этот эффект выражен более четко.

Фиг. 164. К оценке экваториальной выпуклости Земли.

V. Прецессия

Ньютон так объяснил прецессию равноденствий: ось вращения Земли описывает конус, ибо Солнце и Луна притягивают экваториальную выпуклость Земли. Земная ось наклонена к плоскости эллиптической орбиты Земли, поэтому экваториальная выпуклость приводит к несимметричному притяжению Солнцем и Луной. Мы остановимся здесь на эффекте, связанном с притяжением Солнцем. Сферическую Землю Солнце притягивало бы равномерно, как если бы вся масса Земли была сосредоточена в ее центре. Равнодействующая сила в этом случае должна быть направлена по прямой, соединяющей центры Земли и Солнца, независимо от того, вращается Земля или нет (фиг. 166, а ). Сфероид с экваториальной выпуклостью подвергается дополнительным воздействиям, приложенным к выпуклости (фиг. 166, б ).

Фиг. 165. Прецессия равноденствий.

а— шарообразная Земля не прецессировала бы даже совершая суточное вращение; б— через сотни лет Земля вращалась бы по своей орбите с тем же наклоном; в— прецессия сплющенной Земли; г— через несколько столетий ось вращения повернется по поверхности конуса прецессии.

Фиг. 166. Прецессия.

а— Солнце притягивало бы сферическую Землю с силой, действующей по линии, соединяющей центры Земли и Солнца, независимо от того, вращается Земля или нет; б— Солнце притягивает неравномерно выпуклости сплющенной Земли.

Эти малые дополнительные силы не равны — большее притяжение испытывает часть, обращенная к Солнцу (фиг. 167).

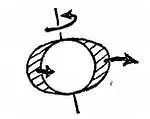
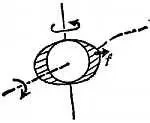
Эти малые дополнительные силы равноценны некоторому добавочному притяжению, направленному по линии, соединяющей центры Солнца и Земли, и небольшой добавочной силе f , которая стремится опрокинуть земную ось.

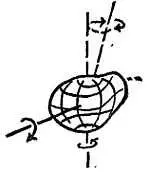
Как и в любом случае вращения тела вокруг собственной оси, действие какой-либо силы, стремящейся наклонить ось вращения, сводится не к наклону оси, а к возникновению прецессии вокруг другой оси.

Фиг. 167. Солнце притягивает ближайшую часть выпуклости сильнее, чем отдаленную.

Дополнительные силы эквивалентны среднему притяжению всей выпуклости, направленному по линии, соединяющей центры, плюс небольшая сила f , которая как бы качает земную ось. Так как земная ось наклонена, эта сила направлена от центра под углом. Угол между земной осью и дополнительной силой больше всего отличается от прямого в середине лета и в середине зимы. Когда такая сила действует на вращающееся тело, она не опрокидывает его, как можно было бы ожидать. Возникает очень интересное движение, называемое прецессией ; вы можете его наблюдать, наклонив ось быстро вращающегося волчка. В этом случае сила тяжести, действующая на волчок, не опрокидывает его, а заставляет ось вращения волчка описывать конус. Ньютон показал, что притяжение Солнца и даже в большей степени Луны вызывает прецессию земной оси по конусу с углом раствора 23 1/ 2° с периодом 26 009 лет (фиг. 167). Наконец было дано объяснение прецессии. Ее наблюдали еще греки, затем пытался объяснить Коперник, но явление оставалось совершенно необъяснимым до Ньютона. Это движение казалось таким непонятным, что почти не было надежды найти ему простое объяснение. Однако Ньютон показал, что это еще одно из проявлений всемирного тяготения: вращающаяся вокруг оси Земля прецессирует подобно волчку.