Эрик Роджерс - Физика для любознательных. Том 2. Наука о Земле и Вселенной. Молекулы и энергия

Так Ньютон перенес простое представление о движении Луны на всю планетную систему. Он предположил, что любое тело притягивается другим с силой, пропорциональной их массам и обратно пропорциональной квадрату расстояния между ними. На основе этой гипотезы он создал подробную картину движения тел в Солнечной системе, свод законов, которые проверялись точными измерениями в течение двух столетий. Спутники планет подчиняются тем же законам. Даже кометы следуют общему правилу. И все эти движения определяются силой тяжести, которая хорошо известна на Земле. Ньютон объяснил небесную систему на основе единой рациональной схемы.

Это столь большое достижение, что следует специально проследить путь, которым Ньютон получил три закона Кеплера и затем использовал их в дальнейшей работе. Первое доказательство того, что движение планеты происходит по эллипсу, можно сделать либо используя изобретенное Ньютоном дифференциальное исчисление, либо опираясь на сложные и громоздкие геометрические доказательства. (Ньютон получил доказательство и геометрическим путем, чтобы убедить в своей правоте противников дифференциального исчисления.) Мы с большим сожалением опускаем это доказательство.

Выведем теперь третий закон Кеплера, а затем второй закон — закон равных площадей за равные времена. Второй закон следует из произвольной зависимости силы притяжения от расстояния, если эта сила действует по прямой, соединяющей центры планеты и Солнца. Но первому и третьему законам Кеплера удовлетворяет только закон обратной пропорциональности сил притяжения квадрату расстояния.

Третий закон Кеплера

Чтобы получить третий закон Кеплера, Ньютон просто объединил законы движения с законом всемирного тяготения. Эллиптические орбиты движения планеты получаются, если использовать методы дифференциального исчисления, учитывающего изменения радиуса и скорости планеты. В результате таких вычислений получится третий закон Кеплера.

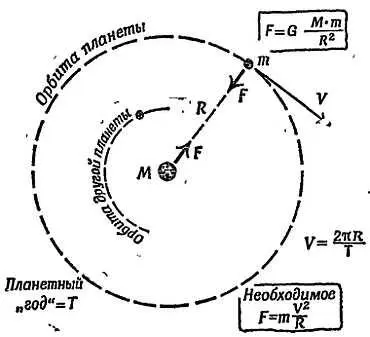
Фиг. 152. Движение планет.

Для случая круговых орбит можно рассуждать следующим образом: пусть планета, масса которой равна m , движется со скоростью v по окружности радиуса R вокруг Солнца, масса которого равна М . Это движение может осуществляться только в том случае, если на планету действует внешняя сила mv 2/ R , создающая центростремительное ускорение v 2/ R (см. гл. 21 ). Предположим, что притяжение между Солнцем и планетой как раз и создает необходимую силу. Тогда

G∙( M∙ m/ d 2) = m∙ v 2/ R

и расстояние d между m и М равно радиусу орбиты R . Но скорость

v= ДЛИНА ОКРУЖНОСТИ / ПЕРИОД ОБРАЩЕНИЯ = 2π R/ T

где Т — время, за которое планета совершает один оборот. Тогда

G∙( M∙ m/ R 2) = [(2π R/ T )2/ R]∙ m; G∙( M∙ m/ R 2) = 4π 2 m∙ R 2/ T 2 R

Чтобы получить третий закон Кеплера, нужно перенести все R и T в одну сторону уравнения, а все остальные величины — в другую:

R 3/ T 2= G∙ M/4π 2

Если перейти теперь к другой планете, с другим радиусом орбиты R ' и периодом обращения Т ', то новое отношение ( R ') 3/( T ') 2будет опять равно G ∙ M /4π 2; эта величина будет одинаковой для всех планет , так как G — универсальная постоянная, а масса М — одна и та же для всех планет, вращающихся вокруг Солнца. Таким образом, величина R 3/ T 2будет одной и той же для всех планет в согласии с третьим законом Кеплера. Для других систем, например для спутников Юпитера, величина М будет другой (в этом случае М — масса Юпитера), a R 3/ T 2будет иметь другое значение, одинаковое для всех спутников.

Масса планеты m сокращается. Несколько планет с различными массами могли выдвигаться по одной и той же орбите. Вы могли бы об этом догадаться — ведь это знаменитый эксперимент, но в космическом масштабе.

Если закон убывания силы тяжести отличается от закона обратных квадратов, то отношение R 3/ T 2не будет одним и тем же для всех планет. Например, если использовать закон обратной пропорциональности кубу расстояния, то для всех планет постоянной будет величина R 4/ T 2; в этом случае величины R 3/ T 2будут пропорциональны 1/ R и для разных планет будут разными. В действительности, как установил Кеплер, эти величины одни и те же. Это означает, что справедлив закон обратных квадратов.

Дифференциальное исчисление позволяет получить третий закон и для эллиптических орбит, но в этом случае R — средняя величина между наибольшим и наименьшим расстоянием планеты от Солнца.

Второй закон Кеплера

Приведем приближенные вычисления, выполненные Ньютоном. Будем основываться на втором законе Ньютона: изменение количества движения равно F ∙Δ t . Следовательно, изменение mv — вектор, направленный по линии действия силы F и пропорциональный ее величине.

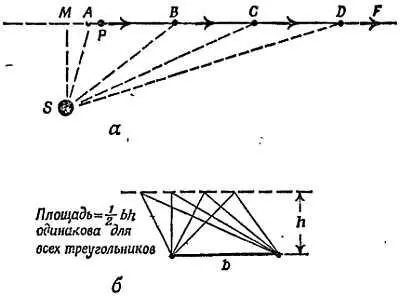
Фиг. 153. Свободное движение планеты.

а— планета Р движется прямолинейно о постоянной скоростью, за равные промежутки времени радиус-вектор описывает равные площади; б— свойства треугольников, которыми мы здесь пользуемся.

Вначале предположим, что планета движется свободно, т. е. на нее не действуют силы. Мы можем провести радиусы, соединяющие планету с Солнцем, лишенным гравитации (фиг. 153). Планета Р будет двигаться с постоянной скоростью по прямой линии AF (первый закон Ньютона). Обозначим расстояния, пройденные планетой за одинаковые интервалы времени: АВ, ВС, CD и т. д. Так как скорость постоянна, то AB = BC = CD и т. д.

Рассмотрим площади, описываемые радиусом SP в процессе движения. Как сравнить треугольники SAB, SBC, SCD ? У всех этих треугольников одинаковые высоты SM и одинаковые основания АВ, ВС, CD . Из этого следует, что площади треугольников равны. Радиус-вектор, проведенный из точки S , описывает одинаковые площади за равные интервалы времени, так что это простое движение подчиняется закону Кеплера.

Теперь предположим, что планета движется по орбите благодаря тому, что Солнце притягивает ее и сила притяжения направлена по радиусу PS . Чтобы упростить геометрическое рассмотрение, предположим, что притяжение действует только в точках А, В, С …. траектории, а остальное время планета движется свободно по прямой линии. Тогда траектория планеты будет выглядеть так, как показано на фиг. 154.