Эрик Роджерс - Физика для любознательных. Том 2. Наука о Земле и Вселенной. Молекулы и энергия

СИЛА∙ВРЕМЯ = ПРИРАЩЕНИЕ КОЛИЧЕСТВА ДВИЖЕНИЯ,

т. е. второму закону Ньютона, будет соответствовать

МОМЕНТ СИЛЫ∙ВРЕМЯ = ПРИРАЩЕНИЕ МОМЕНТА КОЛИЧЕСТВА ДВИЖЕНИЯ.

Задумайтесь над смыслом момента количества движения, и вы, вероятно, придете к правильному заключению: подобно тому как момент силы равен произведению силы на плечо ( F ∙ r ), момент количества движения равен количеству движения , умноженному на плечо ( Mv ∙ r ).

Умножьте F и Mv на плечо относительно выбранной оси, и вы получите вариант второго закона Ньютона для случая вращательного движения. Плечо — это перпендикуляр , проведенный от оси в направлении действия вектора силы или количества движения.

Предположим, что два невращающихся тела сталкиваются и в результате одно из них начинает вращаться. Силы взаимодействия тел равны и противоположно направлены (третий закон Ньютона); плечо относительно произвольной оси для этих сил будет одними тем же. Поэтому моменты силы обоих тел относительно выбранной нами оси будут одинаковы по величине и противоположны по направлению. Приобретенный одним телом при столкновении момент количества движения будет равен по величине моменту количества движения второго тела , а их направления будут противоположными. Следовательно, полный момент обоих тел, приобретенный ими в процессе столкновения, равен нулю. Если одно тело начинает вращаться, другое тоже будет вращаться, но в противоположную сторону, вокруг той же оси. При любом столкновении или другом виде взаимодействия момент количества движения сохраняется , он может только передаваться без потерь или могут возникать равные по величине и противоположные по направлению моменты количества движения.

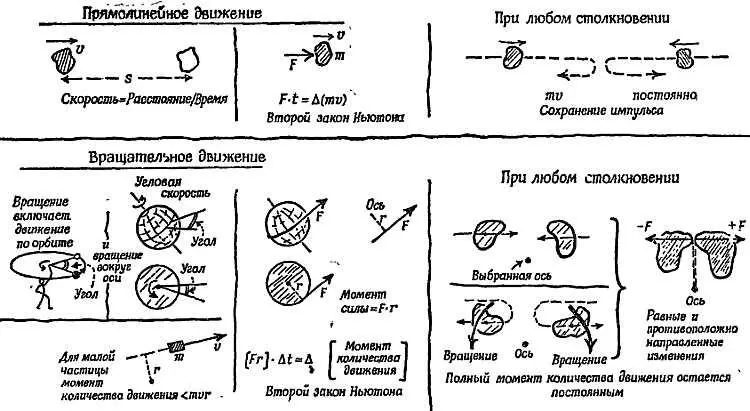
Фиг. 159. Вращения и столкновения.

Ввиду этого вращающееся изолированное тело (например, фигурист, вращающийся на одном коньке) не может изменить своего момента количества движения. Сумма произведений Mv ∙ r , относящихся к различным его частям, не может измениться. Предположим, что тело сжимается (фигурист сводит руки). Тогда величины r убывают для частей тела, приближающихся к оси вращения, и если полный момент остается постоянным, величина Mv должна возрасти — тело начнет вращаться быстрее . Понаблюдайте за фигуристом: независимо от его желания он вращается быстрее, если сводит руки или сгибает вытянутую ногу.

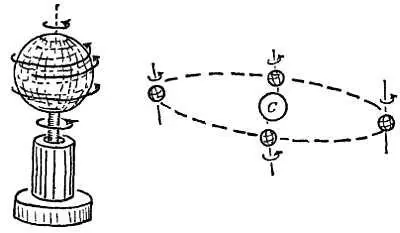
Фиг. 160. Момент количества движения вращающегося вокруг своей оси шара остается неизменным, если к нему не приложен момент внешней силы.

« Изолированное вращающееся тело не может изменить своего момента количества движения». Примените это положение к вращающейся Земле, к человеку на вращающемся без трения стуле. Превратитесь сами в «изолированное вращающееся тело»: начните вращаться, встав на одну пятку так, чтобы вы смогли повернуться несколько раз, прежде чем силы трения остановят ваше движение. (Еще лучше встать или сесть на табуретку, которая свободно вращается.) Возьмите тяжелую книгу и подержите ее на расстоянии вытянутой руки. Теперь, начав вращаться, прижмите книгу быстро к себе. Обратите внимание, как это отразится на вашей скорости. В этом случае момент количества движения сохраняется. Но здесь применим и второй закон Кеплера: книга — «планета», притягиваемая вами — «Солнцем» — во время ее вращения. (В этом опыте участвует ваша масса, которая имеет большую величину, поэтому вы не сможете с достаточной точностью проверить закон Кеплера.)

Для реальной планеты притяжение Солнца не создает момента силы относительно оси, проходящей через Солнце, и, следовательно, не может изменить момент количества движения планеты относительно Солнца . На самом деле последний равен Mv ∙ r , где r — не «рычаг» Кеплера, а отрезок перпендикуляра , опущенного из центра Солнца на касательную к орбите (линию скорости). Когда планета приближается к Солнцу, r уменьшается и, чтобы Mvr было постоянным, v должна возрастать в той же самой пропорции.

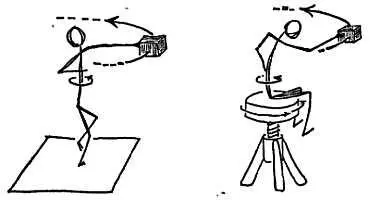
Фиг. 161. Человек на вращающейся площадке увеличивает скорость вращения, когда приближает груз к оси.

Предположим, что за очень короткое время t планета проходит небольшой участок орбиты s со скоростью v= s/ t. На этом участке момент количества движения планеты относительно Солнца равен Mr ∙( s / t ), или Ms ∙ r / t . Но s ∙ r равно произведению высоты на основание малого треугольника , который за время t описывает радиус-вектор. Эта величина равна удвоенной площади треугольника!

Следовательно,

МОМЕНТ КОЛИЧЕСТВА ДВИЖЕНИЯ ПЛАНЕТЫ = (МАССА М)∙(ДВОЙНАЯ ПЛОЩАДЬ, ОПИСЫВАЕМАЯ РАДИУСОМ-ВЕКТОРОМ) / ВРЕМЯ t

Для случая притяжения Солнцем отношение

ОПИСЫВАЕМАЯ ПЛОЩАДЬ/ВРЕМЯ

не меняется: согласно второму закону Кеплера, величина описываемой в единицу времени радиусом-вектором площади не может измениться. Следовательно, когда Кеплер открыл свой второй закон, он показал лишь, что сила притяжения планет направлена точно к Солнцу и что не существует других сил, таких, как трение, обусловленное вязким эфиром.

Закон сохранения момента количества движения столь же универсален, как и другие законы сохранения механики — сохранение массы, количества движения и т. д. В атомной физике мы называем его сокращенно законом сохранения спина и не сомневаемся в его справедливости даже в сложнейших взаимодействиях между частицами и излучением.

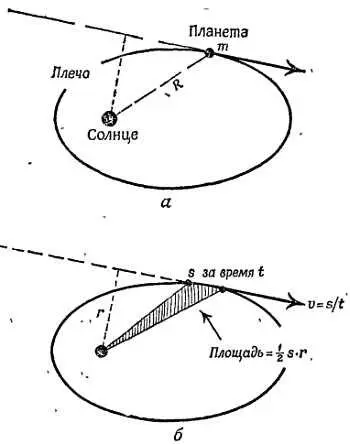
Фиг. 162. Момент количества движения планеты mvr= m∙( s/ t)∙ r= m∙( двойная площадь)/ время.

Плодотворная теория

Ньютон создавал свою теорию последовательно: сформулировал законы движения как исходные пункты разумных предположений, подкрепленных соображениями, полученными из экспериментальных данных; затем получил следствия законов, такие, как законы Кеплера, а затем проверил эти выводы на опыте. В случае законов Кеплера эксперименты уже были сделаны. Наблюдения Тихо Браге были прекрасной проверкой, так что, когда Ньютон получил теоретические результаты, экспериментальная проверка теории уже была заранее готова. Не приходилось поэтому сомневаться в том, что теория «верна». Теория оказалась ценнее отдельных фактов. Она давала ясное и полное представление о движении планет, связывая его с таким привычным явлением, как падение тел. Вооруженный мощными математическими методами и руководимый великолепной интуицией, Ньютон применил свою теорию к большому числу задач, вошедших в его Принципы. Некоторые из этих задач рассмотрены ниже.