Эрик Роджерс - Физика для любознательных. Том 2. Наука о Земле и Вселенной. Молекулы и энергия

Однако сам Ньютон, полный нетерпения, но дальновидный, не был полностью удовлетворен этой проверкой. По непостижимым причинам он отложил все вычисления еще на несколько лет. По-видимому, он стремился решить задачу о притяжении тела шаром с распределенной равномерно в нем массой, подобным Земле. Он уменьшил величину g в 60 2раз, но уменьшение от 1 до (1/60) 2предполагает, что тело на поверхности Земли, для которого ускорение g = 9,81 м/сек 2, находится как бы на расстоянии одного земного радиуса от притягивающего центра. Притягивает ли громадный круглый земной шар яблоко так, как если бы вся масса Земли была сосредоточена в ее центре на расстоянии 6300 км от поверхности? Близкие от яблока части земной массы должны притягивать его очень сильно (согласно закону обратных квадратов).

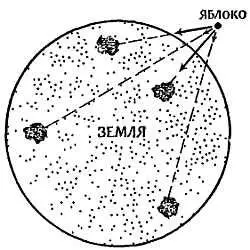
Фиг. 150.Задача Ньютона.

Яблоко, притягиваемое различными частями Земли (показаны четыре отдельных элемента)

Другие части земной массы, находящиеся, например, на расстоянии 12 600 км от яблока, будут притягивать его очень слабо. Сила притяжения различных частей земной массы действует на яблоко под разными углами. Какова результирующая всех этих сил? Здесь мы сталкиваемся с очень трудной математической задачей — сложением бесконечного числа различных притяжений. Она легко решается с помощью интегрального исчисления, но этот тонкий математический аппарат в то время только создавался. Ньютон сам изобрел его для решения этой и других задач, входящих в его работу; одновременно это же сделал и немецкий математик Лейбниц. Его вычисления, связанные с движением Луны, были отложены до тех пор, пока он не убедился, пользуясь изобретенным им методом, что шар с равномерно распределенной массой притягивает тела так, как если бы вся его масса была сосредоточена в его центре, при условии, что каждый участок притягивает тела по закону обратных квадратов . «Как только Ньютон доказал эту замечательную теорему, а мы знаем по его собственным словам, что он и не мечтал получить столь замечательный результат, пока ему не удалось это сделать с помощью собственных математических исследований, весь механизм Вселенной предстал перед ним» [94] J. W. L. Glaisher , On the bicentenary of the Principles, 1887. . После этого он вернулся вновь к изучению движения Луны и с помощью одного лишь расчета проверил свои законы движения, формулу v 2/ R и замечательную идею о законе обратной пропорциональности силы тяжести квадрату расстояния как причины движения Луны по круговой орбите. На сей раз Ньютон был удовлетворен вычислениями. Согласие было полное; необходимая сила получалась за счет уменьшения силы тяжести. Ньютону удалось раскрыть тайну движения Луны.

Объяснение Ньютона

С одной стороны, Ньютон дал объяснение проблеме, предположив, что Луну удерживает на орбите сила тяжести. С другой стороны, он ничего не объяснил. Не была объяснена сущность гравитации, не было высказано никаких соображений относительно того, что же, собственно, представляет собой сила тяжести. Ньютон лишь показал, что одна и та же причина вызывает или обусловливает и падение яблока и движение Луны. Подобное нахождение общих причин нескольких явлений и называется в науке «объяснением».

Если вы разочарованы, то примите во внимание, что такой шаг упрощает картину природы. Заметьте также, что в обычной речи слово «объяснить» означает сделать понимание явлений более простым, ясным. Это объяснение должно также содержать фундаментальные представления, но в работах Ньютона, как и в большинстве наук, основные , или первичные причины не проявляются. Эти работы показали, однако, что явления, которые казались обусловленными различными причинами, тесно связаны между собой. Несмотря на то что мы все глубже изучаем и познаем природу, находя общие связи, основной вопрос о происхождении Вселенной и о том, почему явления в ней протекают именно так, а не иначе, остается пока без ответа.

Всемирное тяготение

Итак, сила тяжести, или, точнее, значительно ослабленная сила тяжести, — вот что удерживает Луну на ее орбите. А как обстоит дело с планетами? Удерживает ли их на орбитах та же сила?

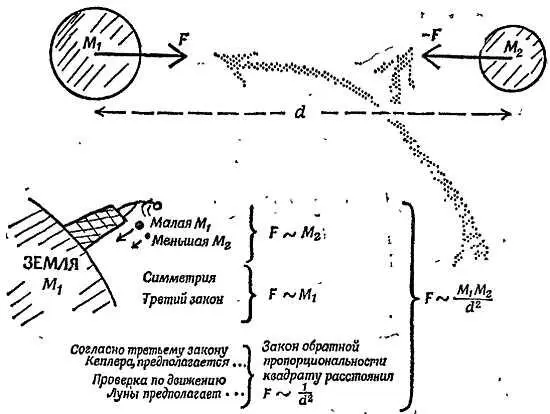
Фиг. 151. Всемирное тяготение.

Поскольку движутся они вокруг Солнца, а не вокруг Земли, то и притягивающая их сила должна исходить от Солнца, а не от Земли. Рассматривая этот вопрос, Ньютон пришел к выводу, что существует всемирное тяготение: все небесные тела испытывают взаимное притяжение, обратно пропорциональное квадрату расстояния. Последнее следовало из анализа третьего закона Кеплера, Ньютон заключил, что любая часть материи во Вселенной притягивается всеми другими телами. Он знал из опыта, что вес тел пропорционален их массе (их притягивает Земля). Следовательно, притяжение Земли изменяется пропорционально массе притягиваемого ею тела. Если, согласно третьему закону, притяжение взаимно, то из соображений симметрии нужно учитывать и М 1— массу Земли, и М 2— массу притягиваемого тела. Зависимость от расстояния была получена с помощью проверки закона обратных квадратов по движению Луны. Поэтому Ньютон включил в общий закон коэффициент 1/ d 2. Вот сформулированный им закон всемирного тяготения:

F~= M 1 M 2/ d 2, или F= ( постоянная )∙ M 1 M 2/ d 2, или F= G∙( M 1 M 2/ d 2),

Где G — универсальная постоянная; М 1и М 2— массы; d — расстояние между ними; F — сила, с которой каждое тело притягивает другое. Нужно помнить, что универсальная постоянная G имеет другой физический смысл, нежели g , — локальное значение ускорения силы тяжести [95] Для случая Земли и яблока М 1 и М 2 — соответственно массы Земли и яблока; расстояние между ними равно радиусу Земли r . Таким образом, вес яблока M 2 g = GM 1 M 2 / r 2 . Отсюда следует связь между g и G : g = G ∙ M 1 / r 2 УСКОРЕНИЕ g = ГРАВИТАЦИОННАЯ ПОСТОЯННАЯ ∙ МАССА ЗЕМЛИ / (РАДИУС ЗЕМЛИ) 2 .

Могут ли эти общие законы объяснить движение планет? Ньютон доказал, что могут. Он показал, что притяжение по выведенным им законам обусловливает движение планет по эллиптическим орбитам, причем в одном из фокусов эллипса должно находиться Солнце. Ему удалось легко вывести два других закона Кеплера, которые также вытекают из его гипотезы всемирного тяготения. (Эти законы справедливы, если учитывается только притяжение Солнцем. Но мы должны учитывать и действие на движущуюся планету других планет.) В Солнечной системе эти притяжения незначительны по сравнению с притяжением Солнца, однако в точных расчетах ими нельзя пренебречь.