Брайан Кокс - Почему Е=mc²? И почему это должно нас волновать

В самом общем виде сила тяжести в разных местах разная. Чем выше вы находитесь над уровнем Земли, тем она меньше, хотя разница между силой тяжести на уровне моря и на вершине Эвереста не такая уж и большая. На Луне сила тяжести гораздо меньше, поскольку масса Луны меньше массы Земли. Аналогично сила притяжения Солнца намного больше, чем сила притяжения Земли. Но где бы в Солнечной системе вы ни находились, сила тяжести в непосредственной близости от вас почти не меняется. Представьте, что вы стоите на земле. Гравитация у ваших ног будет немного сильнее, чем на уровне головы, но разница совсем невелика. Причем она будет меньше для низкорослого человека и больше для высокого. Вообразите крохотного муравья. Разница между силой тяжести у его ног и на уровне головы будет еще меньше. Давайте еще раз отправимся по проторенному пути мысленного эксперимента и станем рисовать себе все более и более мелкие объекты, вплоть до крохотного лифта, который настолько мал, что можно предположить, что сила тяжести в нем повсюду одинакова. В этом крохотном лифте обитают еще более крохотные физики, задача которых – ставить в нем научные эксперименты. А теперь представим, что этот крохотный лифт находится в состоянии свободного падения. В этом случае ни один из крохотных физиков даже не произнес бы слово «гравитация» своим писклявым голосом, так как обнаружить данный эффект посредством наблюдений в лифте невозможно. В описании мира с точки зрения наблюдений, сделанных этой группой крохотных падающих физиков, был бы один поразительный аспект: силы тяжести в нем просто нет. Но подождите-ка! Ведь нечто явно удерживает Землю на орбите вокруг Солнца. Это просто еще один хитрый трюк или в этом есть что-то важное?

Давайте на минуту оставим в стороне силу тяжести и пространство-время и вернемся к искривленной поверхности Земли. Пилот, планирующий перелет из Манчестера в Нью-Йорк, должен учитывать, что поверхность Земли имеет определенную кривизну. С другой стороны, когда вы переходите из столовой на кухню, вам не нужно помнить о кривизне поверхности Земли и вы вполне можете исходить из того, что эта поверхность плоская. Другими словами, геометрия этого участка поверхности очень близка к эвклидовой. По большому счету именно поэтому людям понадобилось так много времени, чтобы открыть тот факт, что Земля не плоская, а круглая: радиус кривизны гораздо больше, чем те расстояния, с которыми люди раньше имели дело. Давайте мысленно разделим поверхность Земли на небольшие квадратные участки, как показано на рис. 25. Каждый участок имеет почти плоскую поверхность, причем чем меньше размер участка, тем он более плоский. На каждом таком участке правит эвклидова геометрия: параллельные прямые не пересекаются и теорема Пифагора работает. Кривизна поверхности Земли становится очевидной, только когда мы пытаемся покрыть большие площади этой поверхности эвклидовыми участками. Для того чтобы построить искривленную поверхность сферы, необходимо соединить вместе огромное множество таких участков.

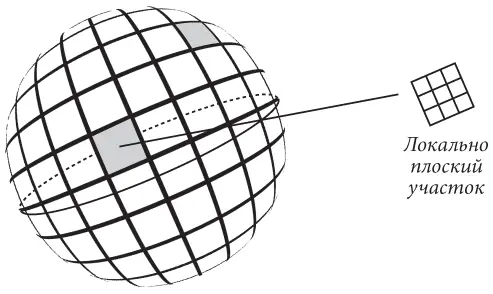
Рис. 25

Теперь давайте вернемся к нашему маленькому лифту, находящемуся в состоянии свободного падения, и представим, что рядом с ним расположено множество других маленьких лифтов – фактически в каждой точке пространства-времени. Внутри каждого такого лифта пространство-время примерно одно и то же, причем чем меньше лифт, тем точнее приближение. А теперь вспомните: в главе 4 мы обращали ваше внимание на предположение, что пространство-время должно быть неизменным и одинаковым повсюду – это было крайне важно для построения формулы расстояния в пространстве-времени Минковского. Поскольку пространство-время внутри каждого крохотного лифта также неизменно и везде одинаково, следовательно, мы можем использовать формулу расстояния Минковского внутри каждого отдельного маленького лифта.

Будем надеяться, что здесь уже начинает возникать аналогия со сферой. Вместо фразы «плоский участок поверхности Земли» следует употребить фразу «падающий лифт в пространстве-времени», а вместо «искривленная земная поверхность» – «искривленное пространство-время». В действительности именно по этой причине физики часто называют пространство-время Минковского плоским пространством-временем. В данной аналогии пространство-время Минковского играет роль эвклидова пространства. В этой книге мы используем слово «плоский» применительно к эвклидовой геометрии, а знак минус, который присутствует в сформулированной Минковским версии теоремы Пифагора, подтолкнул нас к употреблению термина «искривленное пространство-время». Использовать язык порой не так просто, как хотелось бы! Таким образом, совокупность маленьких лифтов относится к пространству-времени, как совокупность маленьких участков – к сфере. В каждом крохотном лифте гравитации нет, но можно представить, как совокупность маленьких участков пространства-времени Минковского образует искривленное пространство-время, аналогично тому, как мы строили криволинейную поверхность Земли из плоских эвклидовых участков. Не будь гравитации, мы могли бы обойтись одним большим лифтом, в котором имеет место геометрия Минковского. Таким образом, мы только что узнали, что при наличии гравитации можем сделать так, чтобы она исчезла, но только ценой искривления пространства-времени. Какой удивительный вывод!

Если взглянуть на ситуацию с другой стороны, то, по всей вероятности, мы открыли тот факт, что сила тяжести – не что иное, как сигнал об искривлении самого пространства-времени. Действительно ли это так и что вызывает подобное искривление? Учитывая, что действие гравитации проявляется только в непосредственной близости от материи, мы можем предположить, что пространство-время искривлено поблизости от материи и энергии, поскольку E = mc ². Мы не упоминали о величине искривления пространства-времени и не будем останавливаться на этой концепции подробно, так как она, как принято говорить в физике, нетривиальна. В 1915 году Эйнштейн написал уравнение, которое позволяет определить, каким именно должно быть искривление пространства-времени при наличии материи и энергии. Это уравнение улучшает старый ньютоновский закон тяготения таким образом, чтобы он автоматически соответствовал специальной теории относительности (закон Ньютона не согласуется с ней). Безусловно, это обеспечивает результаты, очень похожие на действие закона Ньютона в большинстве ситуаций, с которыми мы сталкиваемся в повседневной жизни, но все же подчеркивает тот факт, что теория Ньютона – это только приближение. Для того чтобы проиллюстрировать различия в подходах к пониманию гравитации, давайте посмотрим, как Ньютон и Эйнштейн описали бы движение Земли вокруг Солнца. Ньютон сказал бы нечто в таком роде: «Земля притягивается к Солнцу силой тяжести, и это притяжение мешает ей улететь в космос, заставляя вместо этого двигаться по большому кругу» [61]. Эта ситуация аналогична вращению привязанного к веревке мяча над головой. Такой мяч будет перемещаться по кругу, поскольку натяжение веревки мешает ему двигаться иначе. Если перерезать веревку, мяч сразу же улетит по прямой. Точно так же если бы вам удалось отключить притяжение Солнца, то, как сказал бы Ньютон, Земля отправилась бы по прямой в открытый космос. Описание Эйнштейна было бы совсем другим и выглядело бы примерно так: «Солнце – массивный объект и, будучи таковым, искажает пространство-время вблизи себя. Земля свободно перемещается в космическом пространстве, но искривление пространства-времени заставляет ее двигаться по кругу».