Дэйв Голдберг - Вселенная в зеркале заднего вида. Был ли Бог правшой? Или скрытая симметрия, антивещество и бозон Хиггса

Я понимаю, звучит это дико. Ведь если я говорю «поверните электрон», я на самом деле имею в виду, что мы должны повернуть всю вселенную на один полный оборот, а поскольку по определению полный оборот приведет вселенную именно в ту точку, откуда мы начали, в вашем классическом арсенале, очевидно, нет ничего, что помогло бы с этим справиться.

Ничего страшного. Мы же имеем дело не с классической вселенной. В последней главе мы убедились, что для того, чтобы все «выглядело по-прежнему», с волновой функцией вселенной можно поступить двумя способами. Один, как вы, наверное, и сами понимаете, — умножить на 1. Другой, неожиданный, — умножить на –1. Полный оборот фермиона даст вам –1, а второй оборот — еще раз –1. Перемножьте одно на другое и даже на квантовом уровне все вернется туда, откуда началось. Подобный набор вариантов мы видели в конце предыдущей главы.

Вернер Гейзенберг выразился об этом довольно-таки поэтично:

Следует помнить, что то, что мы наблюдаем — это не природа как таковая, а природа, подвергнутая нашему методу задавать вопросы.

Можно проделать небольшой эксперимент, чтобы убедить собственный мозг, что во вселенной не все так очевидно, каким кажется на первый взгляд. Обычно эту версию эксперимента называют «Тарелкой Фейнмана», однако есть и другие, например, «Ремень Дирака» или «Кватернионное рукопожатие». Можете посмотреть на YouTube, там про них есть отличные ролики.

Тарелка Фейнмана

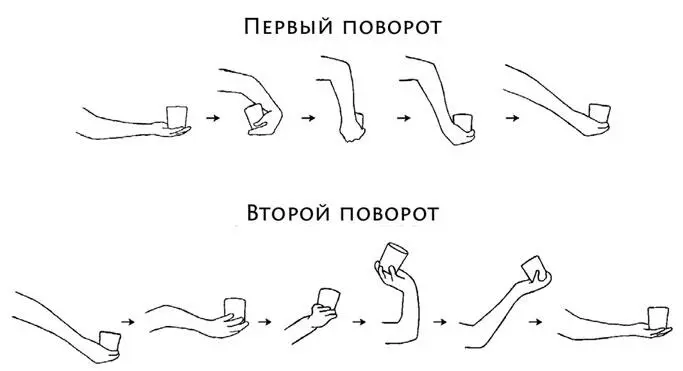
Так вот, я остановлюсь на «Тарелке Фейнмана». Попрошу вас поставить на правую ладонь чашку, полную воды. Очень важно, чтобы в чашке была вода: тогда вы по мокрым коленкам сразу поймете, что эксперимент провалился. Теперь поверните руку в локте на один полный поворот. Осторожно, не пролейте воду. Итак, вы повернули руку на 360 градусов, однако, как вы, наверное, заметили, рука не в том же положении, что до начала движения. Вам неудобно, локоть обращен вверх. Наконец, поверните руку еще на один полной оборот точно так же против часовой стрелки, что и в первый раз, но на этот раз поднимите ладонь и запястье над плечом.

Вуаля! Если вы все сделали правильно, то (1) рука с чашкой окажется совершенно в том же положении, что и в начале, и при этом вы (2) не облились. А главное, чтобы рука очутилась в том же положении, вам понадобилось два оборота.

Электроны — это микроскопические жироскопы, которые каким-то образом, благодаря могуществу матемагии, выглядят по-прежнему, если повернуть их дважды. Однако это свойство, в сущности, просто любопытный факт по сравнению с тем, о чем я сейчас расскажу.

Когда Дирак вывел свойства частиц со спином ‑½, он сделал интересное, но ошибочное заключение. Он решил, будто античастицы якобы выскакивают из уравнений с отрицательной энергией.

Я хочу дать вам представление о том, какой катастрофически нестабильной была бы подобная вселенная. В нашей вселенной электроны и позитроны постоянно возникают из вакуума пространства. В этом нет ничего особенного. Мы уже видели, что эти временные частицы в конечном итоге обеспечивают испарение черных дыр.

С другой стороны, не будь эти частицы временными, у нас появились бы осложнения. Если бы энергия у позитронов была отрицательная, пары создавались бы даром. Вскоре вселенная была бы битком набита веществом, и его некуда было бы девать.

Электроны так себя не ведут, и все тут. Свое знаменитое уравнение Дирак выдвинул в 1928 году, однако двумя годами раньше, еще до того, как поднялся весь этот шум вокруг спина и антивещества, итальянский физик Энрико Ферми — в честь которого, как вы и без меня уже поняли, названы фермионы, — обнаружил, что электроны ведут себя фундаментально иначе, чем частицы вроде фотонов.

Фотоны склонны скапливаться по принципу близости энергий и фаз (именно так устроены лазеры), а электроны, особенно электроны с низкими энергиями, склонны впадать в разные состояния. Именно поэтому бозоны, например, фотоны, и фермионы, например, электроны, рассортировались на разные кучки задолго до того, как мы по-настоящему разобрались в отношениях симметрии, описывающих разницу в их поведении.

Лишь некоторое время спустя мы выяснили, что различие между этими группами частиц, в сущности, сводится к спину. В 1940 году Вольфганг Паули формализовал это различие, сформулировав и доказав теорему о связи спина со статистикой (теорему Паули). В сущности, теорема Паули гласит, что то, бозон перед нами или фермион, целиком и полностью определяет, что происходит, когда подменяешь идентичные частицы в системе.

Чтобы понять, как так получается, нам придется вернуться к волновой природе квантовой механики. У квантовых волн есть несколько важных черт: амплитуда, частота, длина волны и т. д. Однако чаще всего все забывают о так называемой фазе. В любой момент времени в любом месте амплитуда волны может иметь как положительное, так и отрицательное значение в зависимости от того, к чему окажешься ближе, к пику или к минимуму, однако на самом деле нам все равно, потому что единственное, что сыграет роль, это квадрат амплитуды волны. Однако когда волна распространяется, она осциллирует между максимумом и минимумом. Фаза — это просто число, которое описывает, в какой момент мы застали волну.

Фазу легко себе представить по аналогии с пением в канон. Вы начинаете «Братец Яков, братец Яков», а я вступаю через несколько тактов. Канон звучит так красиво именно благодаря разнице фаз .

Квантовая механика идет на шаг дальше. В квантовой механике не просто невозможно измерить фазу волны — фаза вообще не может принимать определенного значения. Если бы могла, у вас были бы все сведения, необходимые для квантовой телепортации, безо всяких досадных помех вроде запутывания, о котором мы говорили чуть раньше. Однако если две волны совпадают или не совпадают по фазе, это нас очень даже интересует. В первом случае волны складываются конструктивно, и вероятности становятся больше, чем были без наложения. Во втором случае они отчасти гасят друг друга. Так и получаются акустические «провалы» в концертных залах [88] Да ладно, что я выпендриваюсь! Мы все в музыке сущие профаны, правда? .

И хотя мы не можем прямо измерить фазу, она наглядно показывает нам, что бывает, когда вращаешь частицу. Если повернуть фермион всего один раз, его волновая функция не совпадет по фазе с отправной точкой на 180 градусов. Это в точности то же самое, что умножить на минус единицу.

Интерференция волн

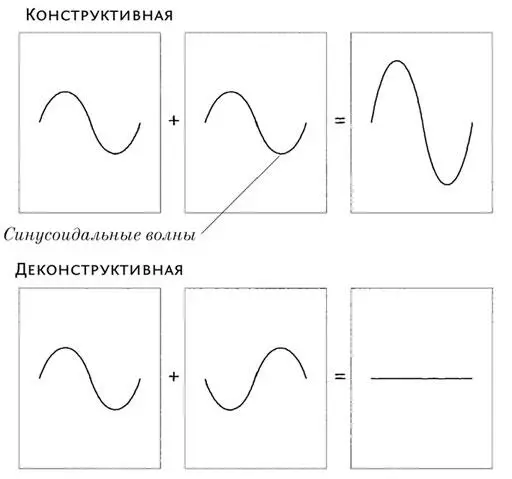
Поверните его второй раз, и получите изменение фазы на 360 градусов, что соответствует полному отсутствию всяких изменений. Именно таков закон для частицы со спином-½.