Лекции по схемотехнике
- Название:Лекции по схемотехнике
- Автор:
- Жанр:
- Издательство:неизвестно
- Год:неизвестен
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Лекции по схемотехнике краткое содержание
Лекции по схемотехнике - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
Элемент ИЛИ-НЕ Рисунок 5,а) осуществляет логическую операцию 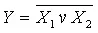 , называемую также стрелкой Пирса. Элемент И-НЕ (Рисунок 5,б) осуществляет логическую операцию
, называемую также стрелкой Пирса. Элемент И-НЕ (Рисунок 5,б) осуществляет логическую операцию  и называется штрих Шеффера. Элемент И-ИЛИ-НЕ (Рисунок 5,в) осуществляет операцию
и называется штрих Шеффера. Элемент И-ИЛИ-НЕ (Рисунок 5,в) осуществляет операцию 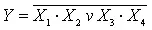 и является элементом сложного базиса.
и является элементом сложного базиса.
Элементы универсальных базисов позволяют реализовать все три основные логические операции (Рисунок 6). Например, для осуществления операции НЕ с помощью элемента И-НЕ достаточно объединить входы 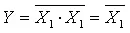 (рисунок 6,а). Аналогично и для элемента ИЛИ-НЕ.
(рисунок 6,а). Аналогично и для элемента ИЛИ-НЕ.
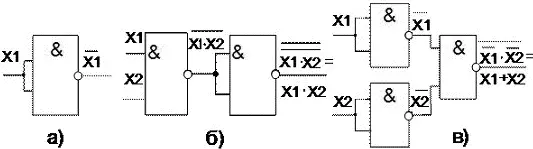
Рисунок 6 Реализация функций НЕ, И и ИЛИ на элементах И-НЕ
При последовательном соединении элемента И-НЕ и инвертора осуществляется операция логического умножения: 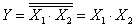 (рисунок 6,б). Такое же соединение элементов ИЛИ-НЕ реализует операцию логического сложения:
(рисунок 6,б). Такое же соединение элементов ИЛИ-НЕ реализует операцию логического сложения: 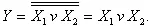
Применение трёх элементов И-НЕ, два из которых работают в режиме инвертирования с объединёнными входами (рисунок 6,в), позволяют реализовать операцию логического сложения 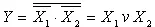 . Соединение трёх логических элементов ИЛИ-НЕ позволяет реализовать операцию логического умножения
. Соединение трёх логических элементов ИЛИ-НЕ позволяет реализовать операцию логического умножения 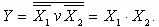
В общем случае логическая функция Y может зависеть от нескольких переменных X 1, X 2,…, X n. Говорят, что функция Y определена, если известны её значения для всех возможных наборов переменных. Функция Y не определена, когда некоторые сочетания переменных по условию задачи невозможны. В этом случае её можно доопределить, приписав ей значение «1» либо «0» по соображениям удобства реализации.
2.4 Минимизация логических формул
Однозначная зависимость сложности логической формулы и функциональной схемы логического устройства приводят к выводу необходимости минимизации структурной формулы логического устройства. Минимизация осуществляется с использованием основных соотношений, законов и теорем алгебры логики.
2.4.1 Расчётный метод минимизации
Применение этого метода состоит в последовательном применении к некоторой формуле законов и правил тождественных преобразований алгебры логики. При этом широко используют следующие приёмы: прибавление одного или нескольких членов, входящих в СДНФ, поскольку X ∨ X ∨ X = X; выделение членов, содержащих множитель 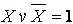 ; использование правила склеивания и др. Получающаяся в результате минимизации алгебраическая формула называется тупиковой. Функция может иметь несколько тупиковых форм.
; использование правила склеивания и др. Получающаяся в результате минимизации алгебраическая формула называется тупиковой. Функция может иметь несколько тупиковых форм.
Пример: Минимизировать функцию СДНФ мажоритарного элемента (См. п.2.2) и реализовать его схему на элементах основного базиса.
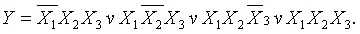
Склеивая первые три минтерма с четвёртым, получаем ДНФ функции мажоритарного элемента, которая проще СДНФ:
Y = X 1· X 2∨ X 1· X 3∨ X 2· X 3
Минимизированная функциональная схема мажоритарного элемента приведена на рисунке 7.
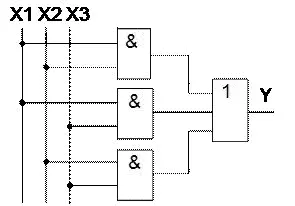
Рисунок 7 Функциональная схема мажоритарного элемента, реализованная на основе минимизированной функции ДНФ
Из сравнения схем, приведённых на рисунках 3 и 7 следует, что в минимизированной схеме число по Квайну уменьшилось с 19 до 9.
Карты Карно — это графическое представление таблиц истинности логических функций. Они содержат по 2 nячеек, где n — число логических переменных. Например, карта Карно для функции трёх переменных содержит 2 n=2 3=8 ячеек, для четырёх переменных — 2 4=16 ячеек.
Карта размечается системой координат, соответствующих значениям входных переменных. Обратим особое внимание на то, что координаты столбцов (а также и строк, если n>3), следуют не в естественном порядке возрастания двоичных кодов, а так: 00 01 11 10. Это делается для того, чтобы соседние наборы (в том числе и столбцов 1 и 4) отличались лишь одной цифрой в каком-либо разряде.
Процесс минимизации заключается в формировании правильных прямоугольников, содержащих по 2 kячеек, где k — целое число. В прямоугольники объединяются соседние ячейки, которые соответствуют соседним элементарным произведениям (т. е. отличаются только в одном разряде).
Несмотря на то, что карты Карно изображаются на плоскости, соседство квадратов устанавливается на поверхности тора. Верхняя и нижняя границы карты как бы склеиваются, образуя поверхность цилиндра. При склеивании боковых границ получается поверхность тора.
Пример: Минимизировать функцию трёх переменных, заданную таблицей истинности (таблица 6).
Таблица 6 Таблица истинности функции трёх переменных
| X1 | X2 | X3 | Y |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 |
СДНФ функции: 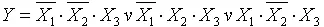
Составляем карту Карно и производим разметку её сторон:
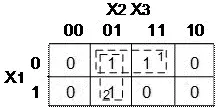
Рисунок 8 Карта Карно функции 3-х переменных.
На карте Карно формируем два прямоугольника. Первый из них объединяет (как бы заключает в скобки) два первых минтерма (слагаемых), а второй — первое и третье слагаемые СДНФ минимизируемой функции, приведённой выше. Минтермы, объединённые в прямоугольники, отличаются только в одном разряде. Их неизменяемая часть, которая при минимизации расчётным методом выносится за скобки, и является минимизированным значением функции:
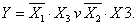
Таким образом, карта Карно позволяет поместить рядом, то есть в соседних ячейках, соседние элементарные произведения, отличающиеся только одним сомножителем.
Читать дальшеИнтервал:
Закладка:






