Александр Астахов - Физика. Порядок вещей, или Осознание знаний. Книга 2

R ср= (А – V * t) / 2 (4.1.2.10)

S = Vл Б* t – а к* t 2/ 2 (4.1.2.11)

Тогда получим для ( а к ):

— а к= 2 * Vл Б /t – 2 * А *ω / t + V *ω (4.1.2.12)

или

— а к= ω * Vр(4.1.2.13)

***

Поскольку формулы ускорения Кориолиса (4.1.2.8) и (4.1.2.13) соответствуют приращению либо только линейной скорости относительного движения по направлению, либо только приращению линейной скорости переносного движения по абсолютной величине, то формулу ускорения Кориолиса намного проще вывести через прирост линейной скорости переносного вращения.

Пусть тело (Б) движется (см. рис. 4.1.2.2) вдоль радиуса в направлении точки (Д) с постоянной радиальной скоростью (Vр). За время (t) – время прохождения пути (БС) линейная скорость движения по окружности увеличится от линейной скорости точки (Б) – (Vлб) до линейной скорости точки (С) – (Vлс). Разгон происходит под воздействием направляющей (ОД) на тело (Б) с силой эквивалентной силе Кориолиса (Fк) и ускорением Кориолиса ( а к ). Ускорение определяется как прирост линейной скорости за единицу времени (t):

а к= (Vл С – Vл Б) / t (4.1.2.14)

Если выразить линейные скорости через угловую скорость получим:

а к= (ω * (А + Vр * t) – ω * А) / t (4.1.2.15)

или:

а к= ω * Vр(4.1.2.16)

В некоторых случаях радиальное относительное движение может осуществляться с ускорением. Это необходимо учитывать при определении ускорения Кориолиса. Рассмотрим случай равноускоренного радиального движения.

Вернемся еще раз к формуле (4.1.2.14):

а к = (Vл С – Vл Б) / t (4.1.2.14)

Запишем выражение для линейной (окружной) скорости в точке (Б):

Vл Б= ω * А (4.1.2.17)

И для линейной (окружной) скорости точки (С):

Vл С= ω * (А + V р* t) (4.1.2.18)

Здесь (Vр) – радиальная скорость с учетом радиального ускорения.

Скорость (Vр) можно найти через радиальное ускорение. Так как ускорение в общем случае может меняться, найдем среднюю величину радиального ускорения ( а р) на участке (БС):

а р= ( а рс+ а рб) / 2 (4.1.2.19)

Тогда радиальная скорость с учетом радиального ускорения определится выражением:

Vр = Vр н+ ( а рс+ а рб) * t/2 (4.1.2.20) где: Vр н – радиальная скорость начальная.

Подставим (4.1.2.20) в (4.1.2.18):

Vл С= ω * (А + (Vр н+ ( а рс+ а рб) * t / 2) * t) =

= ω * А + ω * t * Vр н+ ω * а рс* t 2 / 2 + ω * а рб* t 2/ 2 (4.1.2.21)

Подставим (4.1.2.21) и (4.1.2.17) в (4.14):

а к= ω * А / t + ω * Vр н+ ω * а рс* t / 2 + ω * а рб* t / 2 – ω * А / t

тогда формула для ускорения Кориолиса при ускоренном радиальном движении примет вид:

а к= ω * Vр н+ ω * t * ( а рс+ а рб) / 2 (4.1.2.22)

Как следует из выражения (4.1.2.8) и (4.1.2.16), девиация поворотного движения не зависит от начальной линейной скорости переносного вращения, т.к. начальная скорость есть величина постоянная. Поэтому приращение поворотного движения в каждом минимальном интервале времени, начинающегося не с нулевого радиуса эквивалентно приращению поворотного движения с нулевого радиуса.

***

Аналогичный предыдущему геометрический вывод ускорения Кориолиса приведен в справочнике по физике: Х. Кухлинг, «Справочник по физике», МОСКВА, «МИР», 1983.

«Перемещение тела в радиальном направлении равно r = vt. За то же время точка, удаленная от центра вращения на расстояние r, пройдет по дуге окружности путь s = rωt. Подставив сюда выражение для r, получим s = vtωt = vωt 2. Отсюда следует, что s ~ t 2, т.е. движение происходит ускоренно, а s = аt 2/2. Таким образом, vωt 2= аt 2/2, следовательно, ускорение Кориолиса равно а к= 2vω» (см. Рис. 4.1.8).

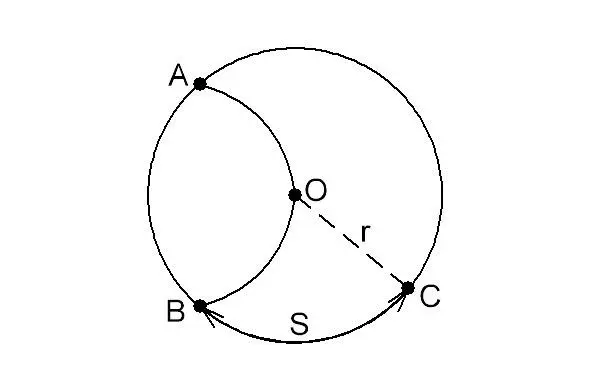
Рис. 4.1.2.3

Как и в большинстве случаев описания физических явлений в современной физике, в выводе Кухлинга какие—либо физические обоснования ускорения Кориолиса отсутствуют. У Кухлинга нет никаких пояснений, из каких соображений путь (s) увязывается с приращением, полученным непосредственно за счет ускорения Кориолиса, кроме некорректной с физической точки зрения фразы:

«За то же время точка, удаленная от центра вращения на расстояние r, пройдет по дуге окружности путь s = rωt».

Точка (В), удаленная от центра вращения на расстояние (r) действительно пройдет указанное Кухлингом расстояние. Однако дуга (ВС) вдвое больше реального пути поворотного движения, что не характерно для девиации, которая эквивалентна только лишь той части реальной траектории, которая пройдена с ускорением. При этом теоретическое обоснование соответствия пути (ВС = s = rωt) девиации поворотного движения у Кухлинга, как и других авторов начисто отсутствует.

***

В приведенных выше двух классических геометрических выводах поворотного ускорения Кориолиса радиальное движение осуществляется в направлении от центра вращения. При движении же к центру вращения подобная логика приводит к полному абсурду.

Пусть, например, тело из точки (Б) (см. рис. 4.1.2.2) движется к центру вращения вдоль направляющей (ДО). В соответствии с классической логикой определения девиации поворотного движения при отсутствии вращения тело (Б) через время (t) оказалось бы в точке (Л). Однако так как направляющая (ДО), вдоль которой движется тело, вращается в направлении (С), то фактически через время (t) тело (Б) окажется в точке (К) пройдя путь равный дуге окружности (КЛ).

Таким образом, в соответствии с классической логикой при радиальном движении к центру вращения за девиацию поворотного движения должна приниматься дуга окружности с минимальным радиусом. Очевидно, что ускорение Кориолиса, определенное через приращение поворотного движения, равного дуге окружности с минимальным радиусом, должно быть вдвое меньше ускорения, определенного через средний радиус и вчетверо меньше классического ускорения Кориолиса.

При этом по логике, заключённой в выводе Кухлинга, в случае нулевого радиуса ускорение Кориолиса также должно быть равно нулю. Однако в реальной действительности в момент перехода через центр вращения ни направление, ни абсолютная величина ускорения Кориолиса не изменяются (см. гл. 8).

Фейнман Р.

Аналитический вывод Фейнмана отличается от приведённых выше геометрических выводов явления Кориолиса тем, что Фейнман определяет ускорение и силу Кориолиса непосредственно через уравнение динамики вращательного движения, минуя геометрические построения.

Ниже приведена фотокопия оригинального текста из работы «ФЕЙНМАНОВСКИЕ ЛЕКЦИИ ПО ФИЗИКЕ. 2. ПРОСТРАНСТВО. ВРЕМЯ. ДВИЖЕНИЕ», стр. 78, 79; Р. Фейнман, Р. Лейтон, М. Сэндс.