Александр Астахов - Физика. Порядок вещей, или Осознание знаний. Книга 2

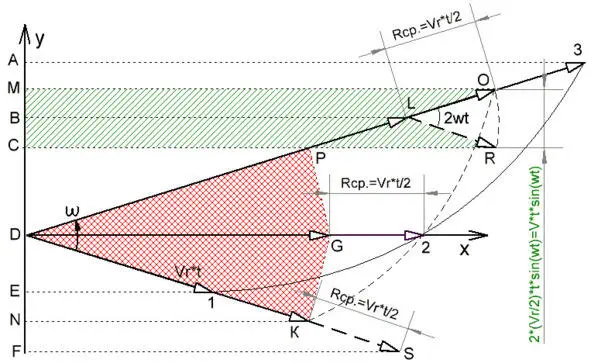
Рис. 4.1.1.4

Как видно, при вычитании смежных участков проекции области (DPG) и (DGK) на ось (Y) взаимно уничтожаются (красная решётчатая штриховка). При этом реальное приращение пути будет вдвое меньшим, чем до коррекции (МD – DE = МС = МВ + ВС = 2 * (Vr / 2) * t * sin (ω * t) = Vr * t * sin (ω * t)) (зелёная косая штриховка). Естественно, что при этом изменятся также и координаты откорректированной схемы. Вместо координат точек («1» «2» «3), равных соответственно (ЕDА) будут координаты точек (K «2» O), равные соответственно (MDN).

Однако в этом нет никакого противоречия, т.к. это уже не траектория реального движения, а эквивалентная схема для вычисления истинного приращения пути. При этом определять новые координаты естественно нет никакой необходимости. Достаточно, математической коррекции полученного по трёхточечной схеме результата. Вывод ускорения Кориолиса через средний радиус будет приведён ниже (см. вывод Кухлинга, гл. 4.1.1.2.).

Таким образом, трёхточечная схема не видит истинную силу Кориолиса-Кеплера. В результате классическое ускорение Кориолиса оказывается завышенным вдвое.

В классической модели явления Кориолиса истинная сила Кориолиса—Кеплера, которая совместно с поддерживающей силой обеспечивает статическую составляющую силы Кориолиса, отсутствует (см. гл. 3.4.3., гл. 4.1.1.). При этом в составе классического ускорения Кориолиса декларируется центростремительное ускорение (ЦСУ) по изменению направления вектора радиальной скорости, которое якобы и приводит к удвоению классического ускорения Кориолиса.

Причём по трёхточечной схеме удваивается в том числе и приращение вращательного движения, которое затем сокращается. Покажем это на рисунке (4.1.1.3).

Приращение пути за счёт ЦСУ равно:

∆Rx = (DL – D «2») – (D”2» – DK) = DL – 2 * D «2» + DK

а = (cos (ωt) * (DL + DK) – 2 * D «2») / t 2

Поскольку DL = DK, а угловая скорость (ω) – постоянная, то

|DL – D «2»| = |D «2» – DK|

Отсюда

DL + DК = 2 * D «2»

Тогда

а = (cos (ωt) – 1) * 2 * D «2») / t 2

Воспользовавшись разложением функции (cos (n) – 1) в ряд Тейлора (cos (n) – 1 = -n 2/ 2…), получаем:

a = – ((ωt) 2 / 2) * 2 * D «2» = ω 2 R,

где D «2» = R

Как видно на рисунке при наличии радиального движения величина приращения (∆Rx) не изменяется, т.к. (-L «2» – «2» K = «2» «3» – «2» «2*»). А вот в тангенциальном направлении ускорение строго зависит от радиального движения, т.к. во-первых, все члены в разностном векторе положительные, а во-вторых, часть поддерживающей силы компенсируется истинной силой Кориолиса-Кеплера. В результате динамическая половина поддерживающей силы обеспечивает только половину классического ускорения Кориолиса.

Для ЦСУ двойка в конечном итоге сокращается, что нивелирует ошибку трёхточечной схемы для движения с центростремительным ускорением. Но то же самое фактически происходит и с ускорением Кориолиса, хотя классическая физика этого почему-то не видит. Если учесть, что половина поддерживающей силы компенсируется за счёт компенсации истинной силы Кориолиса-Кеплера, то двойка в конечном итоге так же, как и в случае с ЦСУ должна сократиться:

а к = 2 * Vr * t * sin (ω * t / 2) / t = Vr * ω

Таким образом, приращение переносной скорости по абсолютной величине, и поворот радиальной скорости по направлению – это одна и та же физическая величина, которая соответствует одному общему ускорению в тангенциальном направлении, вдвое меньшему классического ускорения Кориолиса.

Приведём физический механизм формирования поворотного ускорения Кориолиса, из которого так же со всей очевидностью следует, что это одна и та же физическая величина. (см. Рис 4.1.2.1).

Радиальное движение может изменить своё направление только при взаимодействии тела с вращающимся радиусом в момент, когда он изменяет своё угловое положение по отношению к прямолинейному радиальному движению. При этом взаимодействие тела с радиусом будет происходить по типу отражения (см. Рис 4.1.2.1, положение 2), ускорение которого никто не подразделяет на самостоятельные составляющие в виде ЦСУ по изменению направления радиальной скорости и ускорения, обеспечивающего приращение линейной скорости переносного вращения.

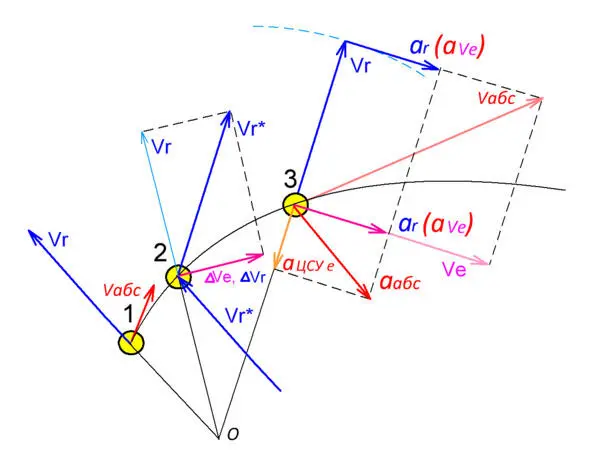
Рис. 4.1.2.1

Оторвавшись после отражения от физического радиуса—направляющей, тело движется по инерции, не меняя больше углового положения и абсолютной величины вектора скорости. При этом тело удаляется от бывшего радиуса вдоль переносной окружности со скоростью, равной проекции своей абсолютной (отражённой) скорости на касательную к окружности текущего переносного вращения.

Одновременно тело удаляется и от центра вращения с радиальной проекцией абсолютной скорости (Vr). При этом угловое положение вращающегося физического радиуса продолжает непрерывно изменяться и после завершения взаимодействия отражения. В результате, физический радиус, который в данном случае совпадает с математическим радиус-вектором постепенно догоняет вектор скорости тела по угловому положению (см. Рис 4.1.2.1).

Очевидно, что все точки вращающегося радиуса имеют свою переносную скорость, которая тем больше, чем дальше она находится от центра вращения. Поэтому, как бы ни была велика отражённая инерционная скорость тела в переносном направлении, одновременно удаляющегося от центра вращения и в радиальном направлении, его рано или поздно настигнет соответственная точка на радиусе, который следует за телом с неизменной угловой скоростью за счёт поддерживающей силы.

Другими словами в процессе радиального движения тело неизбежно переместится в область переносного вращения, в которой тангенциальная скорость точки на радиусе сопоставима со скоростью самого тела в этом направлении, что приведёт к началу нового цикла, но уже на базе новой начальной линейной скорости При этом новое отражение приведёт к новому повороту и новому приращению линейной скорости.

Если при встрече тела с новой точкой радиуса совпадения исходных параметров в виде углового положения и величины вектора скорости не произойдёт, то заработает механизм с отрицательной обратной связью, регулирующий эти параметры. При этом каждое последующее отражение будет происходить при меньшем различии исходных параметров взаимодействия, которые вдруг по какой—либо причине не совпали с «первой попытки». Так будет происходить, вплоть до их полного совпадения.