Аттилио Ригамонти - Физика повседневности. От мыльных пузырей до квантовых технологий

Радуга возникает из-за взаимодействия солнечного света с каплями воды, взвешенными в атмосфере (илл. 8). Эти капли размером порядка 0,1 мм значительно больше, чем длина световой волны. В результате путь световых лучей в каждую каплю может быть описан геометрической оптикой, то есть преломлением на входе и на выходе. Между этими преломлениями внутри капли может произойти одно или несколько отражений. Основная радуга, часто единственная видимая, соответствует одному промежуточному отражению, а иногда появляющаяся вторичная радуга создана лучами, которые претерпели два отражения в каплях воды (илл. 9). Для данной длины волны отклонение светового луча каплей воды зависит от того, в какой точке он в нее попадает, и определяется законами преломления. Однако угол между входящим и выходящим из капли лучами не может принимать любое значение. В случае основной радуги он лежит в диапазоне от 0° примерно до 42°, в чем читатель может убедиться, если не боится вычислений. Отклонения, превышающие 42°, допустимы, но максимальная интенсивность достигается в непосредственной близости от 42°. Для вторичной радуги этот угол составляет около 51°. Поворачиваясь к солнцу спиной, мы наблюдаем две яркие дуги. Между ними появляется темный участок: действительно, никакой луч не появится между двумя критическими углами после одного или двух отражений в каплях воды, и потому эта область выглядит темнее, чем остальная часть неба.

Давайте вспомним закон, названный во Франции законом Снелла – Декарта или просто законом Декарта, а в других странах – законом Снеллиуса (см. главу 2, «Отражение и преломление световых волн»). Декарт, по-видимому, первым опубликовал его в трактате «Диоптрика» в 1637 году, но закон уже был открыт голландским математиком Виллебрордом Снеллом, или Снеллиусом (1580–1626), а до него – персидским ученым Ибн Салемом в конце X века.

Снелл, вероятно, основывался на экспериментальных работах, в то время как Декарт утверждал, что открыл этот закон, приравняв луч света к траектории пули. Это не слишком понятное доказательство было раскритиковано Пьером де Ферма в работе, опубликованной в 1662 году под названием «Сумма о преломлениях» (Synthèse pour les réfractions). Принцип Ферма, изложенный в этом тексте, гласит, что свет проходит по пути, который позволяет ему скорейшим образом перейти от точки А к точке В (см. илл.). Предоставим читателю вывести закон Снеллиуса из принципа Ферма, что не составит труда при наличии некоторого знания тригонометрии и дифференциального исчисления. Просто найдите точку C, которая минимизирует время, затраченное светом, чтобы пройти по пути ABC, – это время равно (AC/ c ) + (BC/ v ), где c – скорость света в воздухе и v = c / n – его скорость в воде.

Если доказательство Декарта любопытно скорее с исторической стороны, то принцип Ферма сохраняет определенный интерес и для современной физики. Кроме того, именно Декарт первым объяснил появление двух радуг и рассчитал соответствующие углы отклонения.

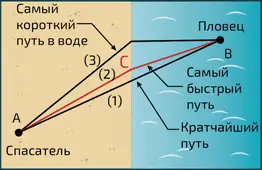
Спасатель (А), которому нужно как можно скорее спасти пловца (B), бежит по пляжу быстрее, чем плывет в море. Самый краткий путь, прямой (1), не будет самым быстрым: спасатель потеряет много времени в море. Если же он максимально сократит время плавания (3), то значительно увеличит путь по пляжу. В итоге самый быстрый путь (2), проходящий через C, – тот, который отвечает закону Снеллиуса

Так объясняется появление световых дуг, но не их цветов… На самом деле точное значение угла отражения зависит от цвета, так как показатель преломления воды n увеличивается, когда длина волны уменьшается. Итак, для фиксированного угла падения i угол преломления увеличивается с длиной волны, то есть двигается от синего к красному. Это значит, что отклонение на входе и выходе капли сильнее для синего, чем для красного. Таким образом, с внешней стороны дуги появляется красный цвет. Все наоборот во вторичной радуге, цвета которой расположены в обратном порядке: красный внутри. Эти вытекающие из геометрии и законов преломления странности – примеры сюрпризов, что порой несут нам научные расчеты.

Рассматривая картину Рылова, мы еще не обсудили птиц, которые составляют неотъемлемую часть обаяния морских берегов. Давайте исправим это упущение такой задачей: как часто птице заданной массы нужно взмахивать крыльями, чтобы лететь? Возможно, читателю трудно будет увидеть связь между этими величинами, и он решит, что авторы играют с ним как кошка с мышкой.

Пусть m – масса птицы, S – общая площадь крыльев, v – средняя скорость крыла, t – продолжительность удара крыла и ρ – плотность воздуха. Во время взмаха крылом птица перемещает воздушную массу, равную M = ρ Svt , и сообщает ей скорость v , что соответствует среднему ускорению v / t , поэтому сила F = Mv / t = ρ Sv 2должна сбалансировать вес mg птицы, где g – ускорение свободного падения. Так,

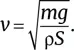
Скорость v крыла пропорциональна количеству взмахов крыльев в секунду υ и длине крыла, которая также пропорциональна 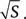Предполагая (довольно произвольно), что коэффициент пропорциональности равен 2π, находим:

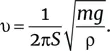
Для серой цапли (илл. 10) масса m составляет порядка 1 кг. Размах ее крыльев – около 2 м, и можно предположить, что площадь S ≈ 0,2 м 2. При приблизительных значениях ρ = 1 кг/м 3и g = 10 м/с 2скорость крыла будет составлять порядка 3 взмахов в секунду, что вполне соответствует реальности между 2 и 3 взмахами в секунду в машущем полете.

10. Площадь крыла серой цапли примерно равна одной десятой квадратного метра

Пойдем дальше и предположим, что все птицы имеют тело той же формы и плотности. Площадь крыльев S в таком случае пропорциональна m 2/3, и из предыдущей формулы следует, что количество взмахов крыльев в секунду обратно пропорционально m 1/6. Действительно, υ уменьшается при увеличении массы птицы: воробей (масса которого составляет порядка 20–30 г) совершает 13 взмахов в секунду, голубь (масса около 500 г) – до 8–9 взмахов, а сарыч (масса примерно килограмм) – до 3.