Аттилио Ригамонти - Физика повседневности. От мыльных пузырей до квантовых технологий

Вышеизложенные соображения делают понятным различие между формой внешнего и внутреннего берегов в излучине, но это еще не все. Как объяснить закон Бэра, согласно которому формы правого и левого берегов различны не только на излучинах? И как объяснить наблюдения географов, которые указывают, что в Северном и Южном полушариях крутость берегов противоположна? Читатель уже догадывается, что здесь, вероятно, играет важную роль вращение Земли, мы вернемся к нему в главе 4, «Возвращение к закону Бэра».

6. Меандр Сены в Лез-Андели, вид на замок Шато-Гайар и остров. Внешний берег крутой, а внутренний – пологий

Форма русла реки во многом зависит от рельефа местности, по которой река протекает. В районе с неоднородным ландшафтом река петляет, избегая неровностей и выбирая путь с наибольшим уклоном. Но и на равнине прямолинейность русла не сохраняется. Небольшой обвал земли или падение дерева на берегу заставляют поток образовать изгиб, который может постепенно увеличиваться, образуя меандр в соответствии с описанным выше процессом.

Какую именно форму обычно принимают меандры реки, текущей по равнине? В 1960-х годах геологи пришли к выводу, что каждая извилина имеет специфическую форму – такую, которую принимает гибкий стержень, если его согнуть, приблизив концы друг к другу (илл. 7). Она представляет собой эйлерову кривую, названную так в честь швейцарского математика Леонарда Эйлера (1707–1783), который первым решил эту задачу. Работа Эйлера по-прежнему широко цитируется в руководствах о прочности балок – те начинают изгибаться, если слишком сильно надавить на их концы (см. врезку в главе 1, «Опыт с продольным изгибом»).

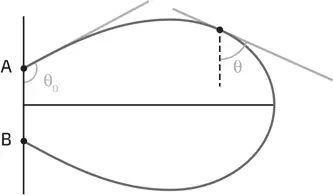
7. Форма, принимаемая упругим стержнем, концы которого зафиксированы в A и B, называется кривой Эйлера. Угол Ѳ между касательной и прямой AB позволяет определить кривизну d Ѳ/ d s, производную от Ѳ относительно пути, пройденного по кривой. Эйлерова кривая минимизирует среднюю квадратичную кривизну стержня, то есть минимизирует интеграл ∫( d Ѳ/ d s) 2 d s, где Ѳ – угол между касательной и некоторым выбранным направлением, а s – длина вдоль кривой. Интеграл берется вдоль всего стержня

Это заключение согласуется с ранее проведенными лабораторными экспериментами, в которых моделировался процесс эволюции русла реки «в идеальных условиях». Оказалось, что в изначально прямолинейном русле очень быстро образуются меандры, хорошо описываемые кривой Эйлера (илл. 8a). Очевидно, что в природе поведение русла реки существенно сложнее «лабораторного» русла (например, из-за неровной местности). И все же подобные структуры, обычно периодические, возникают естественным образом, когда река течет по равнине (илл. 8b). Как правило, чем шире река, тем больше на ней излучин.

Термин «меандры» породила очень извилистая турецкая река Большой Мендерес (тур. Büyük Menderes), название которой происходит от греческого Μαιανδροs («меандрос»). Помимо излучин реки, меандрами называют также извилистые потоки, которые образуются на поверхности ледников, или океанические течения, такие как Гольфстрим.

Для всех этих явлений, происходящих в однородных средах, случайные процессы способствуют образованию более или менее периодических излучин, однако причины их возникновения различны.

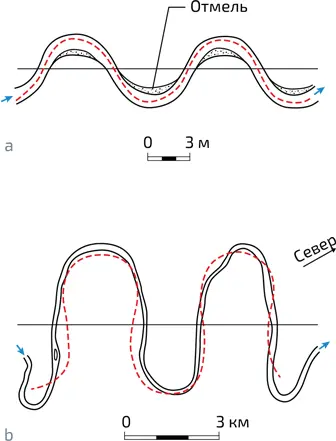
8. а.Меандры, появившиеся в лабораторных условиях в первоначально прямолинейном канале, проложенном в однородной рыхлой среде. Через несколько часов под действием эрозии он изгибается и появляются меандры. Соответствующая кривая Эйлера обозначена пунктиром.

b. Форма природной реки (Потомак в Поу-Поу, США) и ее приближение эйлеровой кривой (пунктирная линия)

Опыт с продольным изгибом

Возьмем плоскую пластиковую линейку, поставим ее на стол и надавим на верхний конец. Пока приложенная сила невелика, линейка остается прямой (см. илл. ниже). Но при определенном давлении линейка сгибается: это явление называется продольным изгибом. Оно возникает, когда сила, действующая на концы, превышает некоторый предел, который тем ниже, чем длиннее и гибче линейка. Очевидно, архитекторы и строители не должны превышать этот предел, когда, например, подпирают террасу металлическими опорами…

В нашем опыте, когда сила воздействия превысила этот предел, линейка согнулась вправо. Но с той же вероятностью она могла бы согнуться и влево! Эту ситуацию можно сравнить с выбором, стоящим перед путешественником, который оказался на незнакомой развилке. Физическое явление, которое открывает две равновероятные возможности изменения какого-либо параметра, ученые называют бифуркацией (от лат. bifurcus – «раздвоенный»).

Явление продольного изгиба

a. До тех пор, пока вертикальная сила F , прилагаемая к линейке, остается меньше предела F 0 , линейка не деформируется.

b. Как только F > F 0 , линейка начнет сгибаться (и даже может сломаться, если сила станет слишком большой).

c. Изменение угла Ѳ 0 , который образует вертикальная линейка в зависимости от величины силы F . Когда последняя достигает величины F 0 , линейка может изогнуться вправо (Ѳ 0 > 90˚) или влево (Ѳ 0 < 0): кривая изменения угла Ѳ 0 имеет две ветви, которые создают бифуркацию

В большое озеро обычно впадает много водных потоков. Например, в Женевское озеро втекает не только Рона, но и небольшие реки, такие как Дранс на юге и Вёвеж на севере. А вытекает из него одна Рона. И это общее утверждение: независимо от количества впадающих в озеро рек, из него никогда не вытекает более одной! Как это объяснить?

Причина заключается в том, что вода из озера вытекает по самому глубокому (низкому) руслу, которое она находит. Если не принимать во внимание исключительные случаи паводков, то обычно поверхность воды в озере находится на уровне самого низкого из возможных мест вытекания, поэтому из него выходит только один поток. Даже если из озера в данный момент вытекает несколько рек, такая ситуация будет нестабильной: ее можно наблюдать только на недавно сформировавшихся озерах. Действительно, самый глубокий поток с более быстрым течением вызовет и более сильную эрозию. В результате его пропускная способность будет увеличиваться, что приведет к снижению уровня озера. Поэтому другие русла будут постепенно мелеть и в конце концов заполнятся грязью. Таким образом, из всех вытекающих из одного озера рек «выживает» только самая глубокая.