Николай Болотов - «Новая Библия» Вселенной

Для особо понятливых поясняю.......Если принять радиус за 1, то длина окружности будет равна 2х3,14…2х3,141…2х3, 1415....длины радиуса, но никогда не закончится неким конечным размером.

Я бы мог привести множество математических постулатов (при отсутствии физических экспериментов) подтверждающих этот наш простецкий вывод.

В частности теорема Бендиксона утверждает, что если мы имеем векторные поля на плоскости в значениях отличных от нуля. в некоторой односвязной области, то в них всегда будут отсутствовать замкнутые фазовые кривые этого поля, целиком лежащие в этой области. При этом в области отсутствуют предельные циклы.

Что дает нам это наше маленькое открытие?

Получается, что любые границы сферы имеют «дырку» в своей оболочке, исходя из того, что число никогда не увеличится до значения длины дуги радиана, кратного длине окружности.

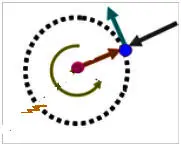
Схематически эта дырка показана на рисунке 15 в виде молниеносного выброса торсионной энергетики волчка физического эфира. Эта точка зрения отражает единство диалектических противоположностей свойств окружности (сферы), которая есть ограниченность и вместе с тем бесконечность!

Объединение двух других противоположностей – замкнутости движения по окружности и безграничности прямолинейного движения – достигается в спирали, что подметил еще Архимед. Это\и объединения нами используется в описанной ниже спиралеобразной модели движения торсионного поля физического вакуума. Архимедова спираль (см. Рисунок 16) и его математическую справочную транскрипцию). При вращении луча против часовой стрелки получается правая спираль (синяя линия), при вращении – по часовой стрелке – левая спираль (черная линия).

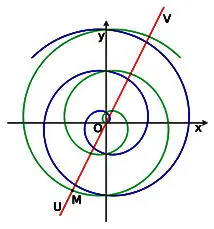
Положительным значениям радиана (ф) соответствует правая спираль, отрицательным – левая спираль.

Если точка M будет двигаться по прямой UV из отрицательных значений через центр вращения O и далее в положительные значения, вдоль прямой UV, то точка M опишет обе ветви спирали. Число a – называется шагом спирали 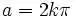. Уравнение Архимедовой спирали можно переписать так: p = ф.

Другими словами, расстояние ρ = OM пропорционально углу поворота φ луча OV. Повороту луча OV на один и тот же угол соответствует одно и то же приращение ρ. Уравнение Архимедовой спирали в полярной системе координат записывается так: Р =kф

При раскручивании спирали, расстояние от точки O до точки M стремится к бесконечности, при этом шаг спирали остаётся постоянным (конечным), то есть, чем дальше от центра, тем ближе витки спирали, по форме, приближаются к окружности.

Вот именно это бесконечное приближение к окружности характеризует фундаментальное свойство замкнутости спиралей волчка физического эфира, о котором мы поговорим ниже.

А сейчас – про свойства двойной спирали Архимеда, которые как нельзя лучше подходят для моделирования процесса расхождения волчка вращения эфира, состоящего из альтернативных торсионных полей (см. рисунок 17).

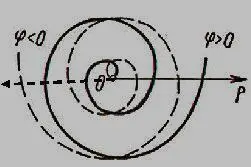
Спираль волчка, раскручиваясь с противоположными значениями радиана (положительном и отрицательном), по философской логике должна формировать альтернативные потоки энергий противоположных не только по направлению вращения и направлениям выхода через «щели нестыковки», заложенные в закономерности вращательного движения, но и объяснять таинственную способность к спонтанному катастрофическому по мощи созидательному процессу формирования физических вселенных.

Вроде той, в которой мы обитаем.

Итак, мы обнаружили «дырку» в геометрии сферы, в которую могут выскользнуть по касательной части вихрей физического вакуума……Но геометрия вращательного движения таит в себе и ещё одну «маленькую тайну». Если вспомнить наши примитивные преобразования в формуле окружности (2R), но с тем условием, что теперь мы примем длину окружности за единицу: 1 = 2R, то R = 1/2.

А это опять иррациональное число, не имеющее конечной (завершающей) длины, примерно такое

0,15915494309189533576888376337251.........

И это значит, что (при несоразмерном радиусе) сфера не имеет постоянно стабильного центра вращения!!!

Я не даром поставил аж 3 восклицательных знака!

При вращательном равномерном движении парадокс нестыковки линейных и угловых функций (из-за хромоватого в своей размерности радиуса) должен приводить к спонтанным нарушениям скорости вращения, а, следовательно, к нарушению баланса двух фундаментальных ускорений вращательного движения (центробежного и центростремительного).

Оттого центр любого вращения генетически лабилен, никоим образом не закреплен и, следовательно, вращение сферы предполагает её спонтанное смешение не только по спирали, но и поступательно.

Следствием этого может стать спонтанное нарушение равновесного вращения волчка эфира с расхождением на два разнонаправленных альтернативных по энергетике вихря, уплотнение которых приводит к формированию материи и антиматерии. То есть не к одинарному взрыву во вселенной, в которой мы живем и который ежедневно наблюдают астрофизики, гадая притом, куда подевалась Антиматерия вместе с Антивселенной, равной по энергии видимой Вселенной. А к двойному, только полностью нами не видимому. Мы видим только «материальный» взрыв, а «антиматериальный» нам лицезреть не дано! Во всяком случае пока что….

Но философское чутьё подсказывает мне, что он должен быть сродни аттрактору (Рис.18) Лоренца – компактному инвариантному множеству в трехмерном фазовом пространстве гладкого потока, которое имеет определённую сложную топологическую структуру и является асимптотически устойчивым.

Не вникая в глубинный сатпматический смысл формулировки, покопавшись в археологии, обнаружил, что спиралеобразные узоры, символизирующие энергию – время, археологи находили на сосудах 4-го тысячелетия до н. э., а также в календаре, вырезанном на бивне мамонта, найденного в Сибири!

Значит, мы не первые!

И это радует, ибо древние люди знали кое-что такое, до чего мы еще не додумались. Наверно, они несли с собой отголоски каких-то очень глубоких знаний предыдущих космических цивилизаций.

Однако всё выше сказанное есть математический домысел (благо математика допускает любую вольность).