Яков Гегузин - Живой кристалл

Яков Ильич основывался на почти самоочевидной, практически единственно разумной по тому времени модели процесса: для того чтобы сдвинуть часть кристалла относительно другой, нужно в плоскости сдвига одновременно перемещать все атомы сдвигаемой части относительно той, которая остается неподвижной. Попросту говоря, для того чтобы сдвинуть, надо сдвинуть! Очень естественное предположение!

Следуя за Френкелем, оценим напряжение, необходимое для этого. Френкель предположил, что по мере перемещения одной части кристалла относительно другой надо преодолевать сопротивление, величина которого со смещением изменяется периодически, повторяясь после каждого смещения на межатомное расстояние. Предположение абсолютно естественное, если только модель, положенная в основу расчета, справедлива. И еще: Френкель предположил, что взаимное смещение частей кристалла сопровождается их упругой деформацией. В этих предположениях он получил оценку того максимального сдвигового напряжения сг т, которое необходимо приложить, чтобы сдвиг начался. А начавшись, он будет продолжаться: в начале процесса, когда атомы сдвигающихся частей кристалла расположены друг над другом, сопротивление сдвигу максимально, а следовательно, лиха беда начало!

Вот френкелевская оценка:

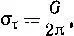
где G — модуль сдвига. Так как G ≈ 10 12дин/см 2, то σ τ= 10 11дин/см 2. В действительности оказывается, что для осуществления сдвига, скажем, кристалла меди достаточно приложить напряжение около 10 8дин/см 2, т. е. в тысячу раз меньшее, чем предсказывает теория, основанная на представлении о сдвиге, который происходит одновременно по всей «плоскости сдвига».

После Френкеля многие теоретики уточняли эту оценку, но их уточнения лишь незначительно изменяли главный результат. Предположение о том, что сдвиг происходит одновременно вдоль всей плоскости, приводит к непомерно большим напряжениям, в тысячи раз превосходящим те, которые обнаруживаются в эксперименте. Френкель оказал огромную услугу проблеме прочности кристалла, вскрыв кричащее противоречие между теорией процесса скольжения и результатами эксперимента.

Теоретик, как правило, более подозреваем в ошибках, чем экспериментатор, который, в отличие от теоретика, свою правоту аргументирует фактами, а не такой зыбкой материей, как рассуждения. Рассуждения обычно считают вещью менее упрямой, чем факт. В случае френкелевской оценки дело обстоит особенно сложно, потому что, казалось бы, невозможно поставить такой опыт, в котором принятая им модель сдвига осуществлялась бы и сделанная оценка была бы экспериментально подтверждена или опровергнута. Действительно, экспериментировать с обычными реальными кристаллами и данном случае нельзя, так как в них практически всегда имеются различные дефекты, а и модель, и расчет Френкеля предполагают кристалл бездефектным, идеальным. И все же возможность осуществить такой эксперимент отыскалась. Он был поставлен почти через 20 лет после френкелевского расчета. В этом опыте экспериментировали не с кристаллами, а с моделью кристалла, построенной из мыльных пузырей.

С пузырьковой моделью БНЛ кристалла мы уже знакомы. Здесь немного скажем только о том, как ею воспользовались для проверки расчета Френкеля. В данном случае модель хороша тем, что она может быть бездефектной, а именно это главным образом и необходимо для проверки правильности расчета.

Моделируя сдвиг в совокупности идеально упорядоченных мыльных пузырьков, экспериментаторы измерили две величины: во-первых, по данным о деформации на самом раннем этапе, когда взаимное соскальзывание пузырьков еще не произошло, они определили модуль сдвига двумерного плота из пузырьков и, во-вторых, по этим же данным определили величину максимального усилия, необходимого для начала собственно сдвига. Оказалось: σ τ = G /20. В знаменателе формулы Френкеля стоит 2π, а у экспериментаторов получилось 20. Расхождению в 3 раза можно не придавать особого значения, тогда как теория с результатами опытов над реальными кристаллами не согласуется в тысячи раз.

Следует обратить внимание на то, что в рассказанной истории модельный опыт сыграл не совсем свойственную ему роль. Он оказался источником информации, которую в опытах с кристаллами ранее получить не смогли. Оказывается, хорошая модель может и это.

Подведем итог. Модельный эксперимент подтверждает справедливость теории, в основе которой лежит представление о том, что сдвиг осуществляется одновременно по всей плоскости. Теория кричаще не согласуется с результатами опытов над реальными кристаллами. Естественно прийти к заключению, что представления, положенные в основу теории, не соответствуют процессам, происходящим в кристаллах, где скольжение происходит как-то не так, как это представлял себе Френкель в 1924 г. Теория явно нуждается в учете реальной структуры кристалла, т. е. факта наличия в кристаллах дефектов. Каких? В каком количестве?

С какими свойствами? До получения ответов на эти вопросы после работы Френкеля прошло 6 лет, в нашей книге все разъяснится в следующем очерке.

В этом очерке должно разъясниться то, что оставалось загадочным в предыдущем. Начнем издалека, с рас-суждений, которые покажутся очень удаленными от интересующего нас кристалла. И для рассуждений изберем модель, к кристаллу не имеющую пи малейшего отношения. Стараясь понять, как происходит скольжение в кристалле, мы будем обсуждать режим движения... гусеницы.

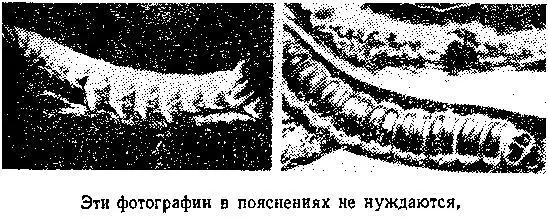
Для начала сделаем с этой «моделью» недобрый эксперимент: попытаемся протащить гусеницу по земле. Сделать это, оказывается, не просто, для этого нужны значительные усилия. Они обусловлены тем, что мы пытаемся одновременно оторвать от земли все пары лапок гусеницы. Вообще говоря, гусеница могла бы перемещаться в таком режиме: одновременно всеми лапками отталкиваться от земли и при этом «проскользнуть» на некоторое расстояние. Каждый такой шаг-скачок требовал бы от гусеницы усилий. На такие усилия она, заведомо, не способна и поэтому пользуется иным режимом движения: от поверхности земли отрывает только пару лапок, переносит их по воздуху, опускает на землю, затем то же повторяет со следующей парой лапок и т. д., и т. д. После того, как каждая пара лапок будет один раз перенесена по воздуху и опущена в новое положение, вся гусеница переместится на расстояние, на которое поочередно смещалась каждая из пар лапок. Это прозвучит курьезно, но гусеничный шаг — это когда гусеница, перемещаясь вдоль земли, в действительности летит по воздуху. Именно так: летит по воздуху! Впрочем, и мы, шагая по земле, летим. Для очередного перемещения ноги мы отрываем ее от земли и с легкостью переносим по воздуху. Ни одну из пар лапок гусеница не волочит по земле. Именно поэтому и ползет легко.