Яков Гегузин - Живой кристалл

Примитивно процесс диффузионного восхождения дислокации можно проиллюстрировать моделью: колодой скользких карт, одна из которых из колоды частично выдвинута. Если такую колоду сжать, выдвинутая карта выскользнет из нее, а если растянуть, карта упадет в колоду.

Не пытаясь строить теорию восхождения дислокаций, а пользуясь только «общими соображениями», можно полагать, что скорость восхождения определяется величиной диффузионного потока атомов к дислокационной линии или от нее. Это означает, что при неизменном напряжении с ростом температуры скорость восхождения будет увеличиваться так же, как и коэффициент диффузии. И расчеты, и опыты согласно свидетельствуют о том, что при температуре, близкой к температуре плавления металлов, дислокация может восходить со скоростью ≈10 - 4см/с. Это — большая величина! Она означает, что за секунду дислокация пройдет путь ≈10 - 4см и пересечет ≈ 10 - 4/ 3 . 10 -8≈ 3 . 10 3атомных плоскостей.

За секунду! Именно поэтому восхождение дислокаций проявляется во многих реальных явлениях и процессах, которые происходят при высоких температурах. Расскажу о двух из них.

Один из процессов заключается в обходе препятствий, которые скользящая дислокация может встретить на своем пути. Представим себе, что к кристаллу извне приложено напряжение, вызывающее в нем скольжение краевых дислокаций вдоль какой-то из плоскостей скольжения. В этой плоскости одна за другой движутся дислокации. В бездефектном кристалле ансамбль скользящих дислокаций напоминает цепочку движущихся друг за другом людей. Именно так по узкой тропинке движутся туристы. Пусть на пути движущихся дислокаций встретится непреодолимый для них барьер. Не важно, что собой представляет этот барьер-стопор, а важно лишь, что для скользящей дислокации он непреодолим. У такого стопора головная дислокация остановится. Скользящие за головной тоже будут тормозиться и поджимать ее к стопору. Дело в том, что две одинаковые дислокации, если они находятся в одной плоскости, друг от друга отталкиваются. Таков закон! Подробно о нем будет рассказано позже, в очерке «Взаимодействие и взаимопревращение дефектов». Этот закон означает, что, приближаясь к себе подобной, движущаяся дислокация будет тормозиться. Испытывая сжимающие напряжения, поджатая к стопору, дислокация начнет диффузионно восходить и перейдет на плоскость, которая расположена над (или под) стопором. На этой плоскости она сможет беспрепятственно продолжать скользить, а кристалл — деформироваться. В этом процессе благодаря восхождению дислокация обходит, огибает стопор, который, скользя, она не могла бы преодолеть. Продолжая аналогию между дислокациями и туристами, уместно вспомнить строку из шуточной песни туристов: «Умный в гору не пойдет, умный гору обойдет!»

Здесь надо упомянуть, что описанный процесс обхода препятствия дислокацией может совершаться при высокой температуре, когда диффузия происходит достаточно быстро. В области низких температур события могут развернуться совсем по-иному... Впрочем, об этом позже, в очерке, посвященном зарождению трещин.

Второй процесс. Он интересен тем, что восхождение дислокаций в нем проявляется в чистом виде, без примеси скольжения. Речь идет о процессе самопроизвольного разгибания некогда согнутого кристалла. Легко представить себе, что к изгибу кристалла приводят незавершенные плоскости, вставленные в кристалл с одной его стороны. Модель: колода карт, в которой некоторое количество карт вставлено не на всю длину колоды. Каждая незавершенная плоскость соответствует одной краевой дислокации. Очевидно, радиус кривизны кристаллической пластинки будет тем меньшим, чем большее число краевых дислокаций одного знака в нем расположено. В процессе отжига эти дислокации расположатся в ряды: это оказывается энергетически выгодным. При этом, однако, число дислокаций останется неизменным, а значит, неизменным останется и кривизна кристалла. Каждый ряд дислокаций подобен сжатой пружине, так как расположенные друг над другом дислокации отталкиваются, — таков закон их взаимодействия. Поэтому дислокации, расположенные над и под средней линией изогнутого кристалла, должны перемещаться к его противоположным поверхностям.

При этом первые (незавершенные плоскости укорачиваются!) становятся «источником» атомов, а вторые (незавершенные плоскости удлиняются!) — «источником» вакансий. Обмениваясь атомами и вакансиями, дислокации диффузионно восходят, через поверхность кристалла выходят за его пределы, их число в кристалле уменьшается, и он разгибается.

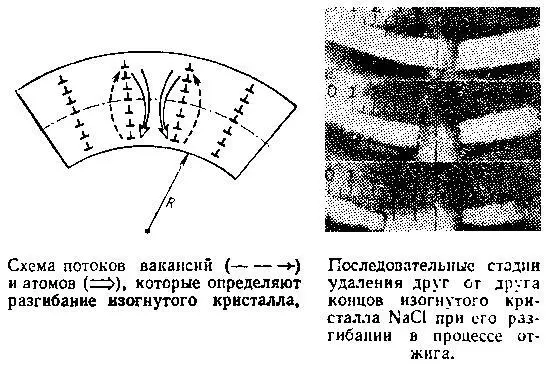
Этот эффект наблюдался в очень простых опытах. Тонкая пластинка монокристалла NaСl изгибалась по кругу так, что между ее концами оставался маленький зазор. Затем она горизонтально располагалась в печи. В процессе отжига велось наблюдение за шириной зазора. Со временем он увеличивался, свидетельствуя о распрямлении кристалла. По скорости распрямления можно было вычислить коэффициент диффузии и убедиться в том, что основной механизм распрямления — это диффузионное восхождение дислокаций.

В истории всякой теории есть период, когда она привлекательна не столько достигнутыми успехами, сколько возникшими перед ней трудностями. Это обычно юношеский период развития теории, когда она испытывает то, что именуется «трудностями роста».

Вопрос «Как растут кристаллы?» тревожил многие умы — и те, которые проблему обсуждали умозрительно, и те, которые, служа практике, пытались лучшим образом искуссвенно выращивать кристаллы.

В нашем повествовании оставим без обсуждения множество наивных догадок о том, как растут кристаллы; эти догадки в ранг теории возводить не надо. Не будучи теориями, они, однако, предшествуют их появлению, и поэтому пренебрежительно перешагивать через эти догадки не следует, они, безусловно, заслуживают благодарности.

Первая серьезная теория роста кристаллов появилась в середине 20-х годов и была предложена немецким физиком Косселем и болгарским физиком Странским. Они рассуждали строго, физически оправданно и очень прямолинейно.

Вот их логика. Есть кристаллик, ограненный плоскими поверхностями. Он играет роль зародыша будущего кристалла, ему надлежит расти. Есть источник атомов, которые, осев на кристалле, увеличивают его объем, способствуют его росту. Атомы могут осаждаться, приходя к зародышу из пересыщенной газовой фазы, или из пересыщенного раствора, или из расплава. До сих пор рассуждения физиков заведомо непорочны, так как ничего, кроме констатации факта, они не содержат: зародыш кристаллика растет за счет осаждения на нем атомов. Теория, однако, обязана предложить модель процесса и ответить на следующие вопросы: в каких случаях атом «сочтет целесообразным» осесть на поверхности растущего кристалла, будет ли он это делать единолично или в компании себе подобных, с какой скоростью кристаллик будет расти, как на эту скорость можно повлиять? У теории можно потребовать ответа еще на многие другие вопросы. Ограничимся этими основными и сочтем теорию разумной, если, в согласии с фактами, она ответит на них.