Яков Гегузин - Живой кристалл

Гриффитс предположил, что в той области нагруженного кристалла, где должно произойти разрушение, сконцентрирована избыточная энергия, величина которой зависит от приложенной к кристаллу нагрузки. При хрупком разрушении эта энергия превращается в энергию образовавшейся поверхности. На языке эксперимента с рогаткой это означает, что часть энергии летящего камня превратилась в энергию поверхностей всех образовавшихся осколков оконного стекла.

Приравняв энергию упругих напряжений, создаваемых в кристалле внешним воздействием, и энергию поверхностей, образующихся при хрупком разрушении, Гриффитс оценил ту прочность, которой должен был бы обладать кристалл. Воспроизведем его расчет, разумеется, в упрощенной форме. Вычислим вначале энергию, сосредоточенную в кубике твердого тела с размером ребра l , который, под действием силы F в направлении ее действия, изменил свой размер на величину Δ l . Сопротивление кристалла деформированию увеличивается с ростом деформации, поэтому сочтем, что среднее значение силы, действующей на кристалл, приблизительно равно F/2. Вспомнив, что работа (или энергия) равна произведению силы на путь, энергию, запасенную в кристалле, определим соотношением

Приравняв упругую энергию поверхностной, Гриффитс нашел формулу, определяющую напряжение σ*, при котором кристалл должен разрушиться (т. е. его теоретическую прочность):

Итак, результат, к которому мы пришли, оказался следующим: ту прочность, которой, согласно расчету, должно обладать вещество, имеют лишь очень тонкие нити из этого вещества, а толстые нити имеют прочность, в 50 — 100 раз меньшую. Такое кричащее несоответствие между теоретической и реальной прочностью твердого тела не может быть обусловлено ошибкой расчета или эксперимента: слишком велико несоответствие, и слишком прозрачны и просты и расчет, и эксперимент. Здесь необходима оговорка. Расчет внушает доверие лишь в случае, если реальная ситуация соответствует той идеализированной, которая в расчете предполагается: твердое тело свободно от каких-либо дефектов, и все связи между атомами, которым надлежит быть разорванными, рвутся одновременно. А вот это, рассуждал Гриффитс, очевидно и не имеет места. Видимо, в реальном твердом теле — в его объеме и на поверхности — имеются микроскопические трещинки. Возможно, именно они и ответственны и за обнаруженное несоответствие теории и эксперимента, и за зависимость прочности нити от ее диаметра. Гриффитс был вынужден придумать дефект и поселить его в твердом теле для того, чтобы помирить теорию и эксперимент. В этом одна из основных забот теоретика — пытаться мирить теорию и эксперимент. Тем более, если теоретик и экспериментатор — одно лицо.

Читатель удивлен, его явно смущает словосочетание «придумать дефект», он, видимо, считает, что ничего придумывать не следует, что поступать надо совсем наоборот — «не поселять» в твердом теле придуманное, а, внимательно изучив структуру твердого тела, обнаружить дефект, наличие которого так резко понижает его прочность. Конечно, хорошо бы поступать так, как рекомендует читатель. Однако в его разумной рекомендации имеется одна логическая брешь. Если дефект будет непосредственно обнаружен, то, следовательно, в кристалле он присутствует. Если же он не будет обнаружен — это не значит, что его в кристалле нет. Это просто значит, что он не был обнаружен, и не более того! Именно такая трудность и встретилась Гриффитсу, не видевшему нужных ему трещин. В этом случае фантазия ученого должна домыслить необнаруженное в надежде на то, что со временем, когда экспериментальные методы станут более совершенными, можно будет убедиться в разумности домысла. Здесь в игру вступает такая тонкая материя, как интуиция ученого, его способность проникать в существо явлений природы, его фантазия, питающаяся знаниями, аналогиями, воспоминаниями, смелостью и независимостью суждений. Гриффитс явно был одарен этими ценностями, потому что, не видя ультрамикроскопических трещин, он их домыслил, а уже затем они были обнаружены и косвенно, и непосредственно.

Предложенный Гриффитсом энергетический подход к описанию разрушения хрупкого твердого тела можно использовать для определения размера той трещинки l *, которая окажется очагом разрушения, если к телу приложено определенное напряжение σ 0.

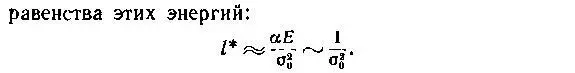
Если трещина имела размер l *или достигла этого размера, ее дальнейшее подрастание будет выгодным, так как при l > l *упругая энергия с ростом l уменьшается быстрее, чем возрастает поверхностная.

Из приведенной оценки l *~ 1 /σ 2 0следует, что с ростом приложенного напряжения размер опасной трещины быстро уменьшается. Та трещина, которая при данном напряжении могла существовать в кристалле, не обнаруживая себя, при немного большем напряжении перейдет в разряд развивающихся трещин, которые себя обнаруживают очень впечатляющим образом: из-за них кристалл рушится. Из нашей оценки l *следует, что в кристаллах, модуль упругости которых Е ≈ 10 12дин/см 2, при напряжении σ 0≈ 10 9дин/см 2все те трещины, размер которых l < 10 -3см, не должны развиваться, опасны лишь те трещины, размер которых превосходит 10 -3см. А вот при напряжении σ 0≈ 10 10дин/см 2опасными окажутся трещинки, размер которых превосходит 10 -5см.

Формулу, которая определяет величину l *, стоит использовать еще и для других оценок, прочтя ее для этого как бы в обратном направлении. Из этой формулы следует оценка напряжения, достаточного для того, чтобы тело, содержащее трещину с размером l *, разрушилось:

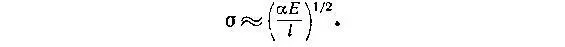
Если бы тело было абсолютно свободно от каких-либо трещин, оно обладало бы «теоретической прочностью» σ*, величинакоторой, как известно, близка к модулю упругости. На этом основании можно получить формулу