Александр Китайгородский - Физика для всех. Движение. Теплота

Несравненно более высокие температуры возникают при взрыве атомной бомбы. По косвенным оценкам, температура в центре взрыва достигает многих миллионов градусов.

В самое последнее время предприняты попытки получить такие сверхвысокие температуры в специальных лабораторных установках (Огра, Зета), изготовляемых у нас и за рубежом. На кратчайшее мгновение удавалось достигнуть температур до двух миллионов градусов.

Сверхвысокие температуры существуют и в природе, но не на Земле, а на других телах Вселенной. В центрах звезд, в частности Солнца, температура достигает десятков миллионов градусов.

Поверхностные же участки звезд имеют значительно более низкую температуру, не превышающую 20 000°. Поверхность Солнца нагрета до 6000°.

Свойства идеального газа, давшего нам определение температуры, очень просты. При постоянной температуре действует закон Бойля – Мариотта: произведение pV при изменениях объема или давления остается неизменным. При неизменном давлении сохраняется частное V / T , как бы ни менялись объем или температура. Эти два закона легко объединить. Ясно, что выражение рV / Т остается тем же, как при постоянной температуре, но изменяющихся V и p , так и при постоянном давлении, но изменяющихся V и T . Выражение pV / T остается постоянным при изменении не только любой пары, но и одновременно всех трех величин – р , V и T . Закон ( pV )/ T = const, как говорят, определяет уравнение состояния идеального газа.

Идеальный газ выбран в качестве термометра потому, что только его свойства связаны с одним лишь движением (но не с взаимодействием) молекул.

Каков же характер связи между движением молекул и температурой? Для ответа на этот вопрос надо найти связь между давлением газа и движением в нем молекул.

В сферическом сосуде радиуса R заключено N молекул газа (рис. 95). Последим за какой-либо молекулой, например той, что движется в данный момент слева направо вдоль хорды длиной l . На столкновения молекул обращать внимания не будем: такие встречи не сказываются на давлении. Долетев до границы сосуда, молекула ударится о стенку и с той же скоростью (удар упругий) понесется уже в другом направлении. В идеале такое путешествие по сосуду могло бы продолжаться вечно. Если v – скорость молекулы, то каждый удар будет происходить через l / v секунд, т.е. в секунду каждая молекула ударится v / l раз. Непрерывная дробь ударов N молекул сливается в единую силу давления.

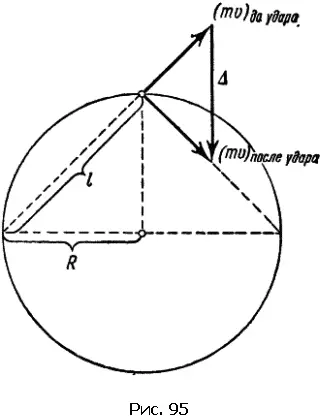
По закону Ньютона сила равна изменению импульса в единицу времени. Обозначим изменение импульса при каждом ударе через Δ. Это изменение происходит v / l раз в секунду. Значит, вклад в силу со стороны одной молекулы будет (Δ/ l )· v .

На рис. 95 построены векторы импульсов до и после удара, а также вектор приращения импульса Δ. Из подобия возникших при построении треугольников следует: Δ/ l = mv / R . Вклад в силу со стороны одной молекулы примет вид:

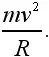
Так как длина хорды не вошла в формулу, то ясно, что молекулы, движущиеся по любой хорде, дают одинаковый вклад в силу. Конечно, изменение импульса при косом ударе будет меньше, но зато удары в этом случае будут чаще. Расчет показал, что оба эффекта в точности компенсируются.

Так как в сфере N молекул, то суммарная сила будет равна:

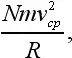
где v ср– средняя скорость молекул.

Давление р газа, равное силе, поделенной на площадь сферы 4π R 2, будет равно:

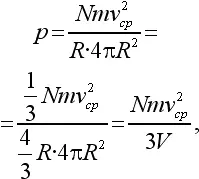
где V – объем сферы.

Таким образом,

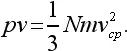
Это уравнение было впервые выведено Даниилом Бернулли в 1738 г. *11.

Из уравнения состояния идеального газа следовало: pV = const· T ; из выведенного уравнения видим, что pV пропорционально v ср 2. Значит,

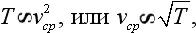
т.е. скорость молекулы идеального газа пропорциональна корню квадратному из абсолютной температуры.

Пусть вещество представляет собой смесь различных молекул. Нет ли такой физической величины, характеризующей движение, которая была бы одинакова для всех этих молекул, например для водорода и кислорода, находящихся при одинаковой температуре?

Механика дает ответ на этот вопрос. Можно доказать, что одинаковыми у всех молекул будут средние кинетические энергии поступательного движения mv ср 2/2 .

Это означает, что при данной температуре средние квадраты скорости молекул обратно пропорциональны массе частиц:

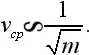
Вернемся теперь к уравнению pV = (1/3) Nmv ср 2. Так как при данной температуре величины mv ср 2одинаковы для всех газов, то число молекул N , заключенных в данном объеме при определенных давлении p и температуре T , одинаково для всех газов. Этот замечательный закон был впервые сформулирован Авогадро.

Сколько же молекул приходится на 1 см 3? Оказывается, в 1 см 3при 0 °C и 760 мм Hg находится 2,7·10 19молекул. Это огромное число. Чтобы вы почувствовали, сколь оно велико, приведем такой пример. Положим, что газ удаляется из маленького сосудика объемом 1 см 3с такой скоростью, что в каждую секунду уходит миллион молекул. Нетрудно подсчитать, что сосуд полностью освободится от газа через миллион лет!

Закон Авогадро указывает, что при определенных давлении и температуре отношение числа молекул к объему, в котором они заключены, N / V есть величина, одинаковая для всех газов.

Так как плотность газа ρ = ( N / V ) m , то отношение плотностей газов равно отношению их молекулярных весов:

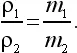
Относительные веса молекул могут быть поэтому установлены простым взвешиванием газообразных веществ. Такие измерения сыграли в свое время большую роль в развитии химии и имеют значение и сейчас, когда нужно найти молекулярный вес нового синтезированного вещества: надо только перевести его, не испортив, в газообразное состояние. Воздух есть смесь газов, и для того, чтобы сравнивать его плотность с плотностью других газов, удобно ввести средний молекулярный вес воздуха. Он оказывается равным 28,8. Зная эту цифру, легко находить плотность различных газов по отношению к воздуху. Например, водяной пар с молекулярным весом 18 имеет по отношению к воздуху плотность 18/28,8 = 0,62.