Александр Китайгородский - Физика для всех. Движение. Теплота

Теория указывает, что при одной температуре средние кинетические энергии молекул mv ср 2/2 одинаковы. При нашем определении температуры эта средняя кинетическая энергия поступательного движения молекул газа пропорциональна абсолютной температуре. В виде равенства этот важнейший закон записывается так:

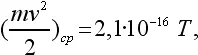
где энергия измеряется в эргах.

Мы уже поняли ранее, что температура является какой-то мерой интенсивности теплового движения. Теперь же мы видим, что измерение температуры термометром, заполненным идеальным газом, придает этой мере на редкость простой смысл. Температура пропорциональна среднему значению энергии поступательного движения молекул.

Определим среднюю скорость молекул кислорода при комнатной температуре, которую мы для круглого счета примем в 27 °C = 300 K. Молекулярный вес кислорода 32, так что вес одной молекулы равен 32/6·10 23. Простое вычисление даст v ср= 4,8·10 4см/с, т.е. около 500 м/с. Существенно быстрее движутся молекулы водорода. Их массы в 16 раз меньше и скорости в sqrt(16) = 4 раза больше, т.е. при комнатной температуре составляют около 2 км/с. Прикинем, с какой тепловой скоростью движется маленькая, видимая в микроскоп частичка. Обычный микроскоп позволяет увидеть пылинку диаметром в 1 микрон (10 −4см), Масса такой частицы при плотности, близкой к единице, будет что-нибудь около 5·10 −13г. Для ее скорости получим около 0,5 см/с. Неудивительно, что такое движение вполне заметно.

Скорость броуновского движения горошины с массой в 0,1 г будет уже всего только 10 −6см/с. Немудрено, что мы не видим броуновского движения таких частиц.

Мы говорили о средних скоростях молекулы. Но ведь не все молекулы движутся с одинаковыми скоростями, какая-то доля молекул движется быстрее, а какая-то медленнее. Все это, оказывается, можно рассчитать. Приведем только результаты.

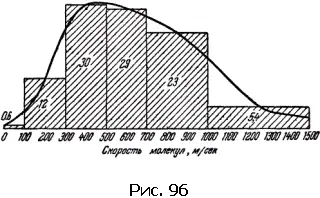
При температуре около 15 °C, например, средняя скорость молекул азота равна 500 м/с; со скоростями от 300 до 700 м/с движется 59 % молекул. С малыми скоростями – от 0 до 100 м/с – движется всего лишь 0,6 % молекул, Быстрых молекул со скоростями свыше 1000 м/с в газе всего лишь 5,4 % (рис. 96).

Можно рассчитать и распределение молекул по разным значениям энергии поступательного движения.

Число молекул, энергия которых более чем в два раза превосходит среднюю, уже меньше 10 %. Доля еще более «энергичных» молекул тает по мере увеличения энергии во все возрастающей степени. Так, молекул, энергия которых в 4 раза больше средней, – всего 0,7 %, в 8 раз больше средней – 0,06·10 −4 %, в 16 раз больше средней – 2·10 −8 %.

Энергия молекулы кислорода, движущейся со скоростью 11 км/с, равна 32·10 −12эрг. Средняя энергия молекулы при комнатной температуре равна всего 6·10 −14эрг.

Таким образом, энергия «одиннадцатикилометровой молекулы» по крайней мере в 500 раз больше энергии молекулы со средней скоростью. Неудивительно, что доля молекул со скоростями выше 11 км/с равна невообразимо малому числу – порядка 10 −300.

Но почему нас заинтересовала скорость 11 км/с? На стр. 161мы говорили о том, что оторваться от Земли могут лишь тела, имеющие эту скорость. Значит, забравшиеся на большую высоту молекулы могут потерять связь с Землей и отправиться в далекое межпланетное путешествие, но для этого надо иметь скорость 11 км/с. Доля таких быстрых молекул, как мы видим, настолько ничтожна, что опасность потери атмосферы Земле не грозит даже через миллиарды лет.

Скорость ухода атмосферы необычайно сильно зависит от гравитационной энергии γ( Mm / r ).Если средняя кинетическая энергия молекулы во много раз меньше гравитационной энергии, то отрыв молекул практически невозможен. На поверхности Луны гравитационная энергия в 20 раз меньше, что дает для энергии «убегания» молекулы кислорода значение 1,5·10 −12эрг. Это значение превышает величину средней кинетической энергии молекулы всего лишь в 20–25 раз. Доля молекул, способных оторваться от Луны, равна 10 −17. Это уже совсем не то, что 10 −300, и подсчет показывает, что воздух будет довольно быстро уходить с Луны в межпланетное пространство. Неудивительно, что на Луне нет атмосферы.

Если нагреть тело, то движение атомов (молекул) будет более интенсивным. Они станут расталкивать друг друга и займут больше места. Этим и объясняется хорошо известный факт: при нагревании твердые, жидкие и газообразные тела расширяются.

О тепловом расширении газов долго говорить не приходится: ведь пропорциональность температуры объему газа была положена в основу нашей температурной шкалы.

Из формулы V = ( V 0/273)· Т мы видим, что объем газа при постоянном давлении возрастает при нагревании на 1 °C на 1/273 часть (т.е. на 0,0037) его объема при 0 °C (это положение иногда называют законом Гей-Люссака).

В обычных условиях, т.е. при комнатной температуре и нормальном атмосферном давлении, расширение большинства жидкостей раза в два-три меньше расширения газов.

Мы уже не раз говорили о своеобразии расширения воды. При нагревании от 0 до 4 °C объем воды уменьшается с нагреванием. Эта особенность в расширении воды играет колоссальную роль в жизни на Земле. Осенью по мере охлаждения воды верхние остывшие слои становятся плотнее и погружаются на дно. На их место снизу поступает более теплая вода. Но такое перемешивание происходит только до тех пор, пока температура воды не понизится до 4 °C. При дальнейшем падении температуры верхние слои уже не будут сжиматься, значит, не будут становиться тяжелее и не станут опускаться на дно. Начиная с этой температуры, верхний слой, постепенно охлаждаясь, доходит до нуля градусов и замерзает.

Только эта особенность воды и препятствует промерзанию рек до дна. Если бы вода вдруг потеряла свою замечательную особенность, даже при скромной фантазии легко представить себе бедственные последствия этого.

Тепловое расширение твердых тел существенно меньше, чем тепловое расширение жидкостей. Оно в сотни и тысячи раз меньше расширения газов.

Во многих случаях тепловое расширение является досадной помехой. Так, изменение размеров движущихся частей часового механизма с переменой температуры привело бы к изменению хода часов, если бы для этих тонких деталей не применялся особый сплав – инвар (инвариантный в переводе означает неизменный, отсюда и название «инвар»). Инвар – сталь с большим содержанием никеля – широко применяется в приборостроении. Стержень из инвара удлиняется лишь на одну миллионную долю своей длины при изменении температуры на 1 °C.