Виктор Бродянский - Вечный двигатель — прежде и теперь. От утопии — к науке, от науки — к утопии

L = Q 1∙(T 1– T 2)/T 1 (3.1)

Здесь, как и на рис. 3.1, высокая температура Т 1в Кельвинах соответствует подводу теплоты Q 1к двигателю, а более низкая Т 2— та, при которой теплота отдается. Из формулы (3.1) прямо следуют многие важные следствия. Для нас имеют значение два вывода.

Первый вывод состоит в том, что получаемая работа всегда меньше подводимой к двигателю теплоты Q. Действительно, коэффициент Карно (Т 1— Т 2)/Т 1(или 1 — T 2/T 1) всегда меньше единицы. Другими словами, в работу может быть превращена только часть получаемой теплоты; другая часть, равная Q 2= Q 1— L, неизбежно должна быть отдана какому-либо теплоприемнику [48] Здесь и в дальнейшем «теплоприемником» будет называться объект (например, атмосферный воздух), к которому отводится теплота от двигателя, а «теплоотдатчиком» — тот, от которого двигатель получает теплоту. при температуре Т 2. Чем выше температура Т 1и ниже Т 2, тем большая доля теплоты Q 1может быть превращена в работу. Но всю теплоту Q 1в работу преобразовать нельзя (для этого Т 1должна была бы быть бесконечно большой или Т 2бесконечно малой).

Так, например, если Т 1= 1200 К, а T 2= 300 К, то из 100 кДж теплоты может быть получено (1200 – 300)/1200 кДж = 75 кДж работы. Остальные 25 кДж могут быть отведены только в виде теплоты Q 2< Q 1при температуре Т 2= 300 К.

Таким образом, из принципа Карно следует, что превратить теплоту в работу полностью нельзя. Следовательно, в природе существует асимметрия во взаимной превратимости теплоты и работы: работа в теплоту может превратиться полностью, но теплота в работу — только частично. Другая, непревратимая часть теплоты неизбежно отводится из двигателя к теплоприемнику (но при более низкой температуре).

Второй вывод из принципа Карно состоит в том, что получение работы из теплоты возможно только в том случае, когда между теплоотдатчиком и теплоприемником есть разность температур (т. е. Т 1> T 2). Действительно, из формулы (3.1) следует, что чем меньше разность Т 1— Т 2, тем меньшая доля теплоты Q может быть превращена в работу. Если же Т 1= Т 2, т. е. если двигатель вступает в тепловой контакт с телами, имеющими одну и ту же температуру, то никакой работы он произвести не может (Т 1— T 2= 0, и, следовательно, L = 0 при любом Q).

Никакими ухищрениями обойти оба эти следствия из принципа Карно нельзя.

Второй вывод из принципа Карно убивает наповал идею о двигателе, работающем за счет теплоты, получаемой из равновесной окружающей среды (ppm-2).

Как бы ни была велика связанная с хаотическим тепловым движением молекул внутренняя энергия, содержащаяся в окружающей среде [49] Ее часто называют «теплотой окружающей среды», но это неверно, как мы уже показали в гл. 2, ибо теплота «содержаться» в окружающей среде (как и в любом другом теле) не может. , она неработоспособна, ибо в этом случае в нашем распоряжении есть только одна температура — окружающей среды T О.С..

Таким образом, само по себе наличие энергии еще не говорит о том, что может быть получена работа: энергия может быть и неработоспособной. Поэтому определение энергии, которое еще встречается в некоторых книгах и даже учебниках, как «величины, характеризующей способности тела (или системы) производить работу», в общем случае неверно. Оно досталось по наследству от XVII-XVIII вв., когда представление об энергии (по тогдашней терминологии — «силе») было связано только с механической работой. Принцип Карно ясно показывает, что такое определение (во всяком случае, применительно к внутренней энергии тела и к теплоте, отводимой от него) неверно.

Вокруг нас в воздухе, воде, почве содержится гигантское количество внутренней энергии хаотического молекулярного движения, но, увы, она вопреки надеждам изобретателей ppm-2 для получения работы абсолютно бесполезна. Это утверждает принцип Карно, вытекающий из второго закона термодинамики.

Из всего изложенного неизбежно следует, что единственный способ обоснования возможности «извлекать тепловую энергию из окружающего пространства» и получать из нее работу состоит в низвержении второго закона термодинамики. Вокруг этой крепости — второго закона — и развертывают все баталии изобретатели и теоретики ppm-2.

Чтобы разобраться во всем этом и показать безнадежность попыток опровергнуть второй закон, нужно рассмотреть некоторые его положения, не ограничиваясь принципом Карно. Особое внимание следует уделить вопросу об энтропии — величине, занимающей центральное место в концепции второго закона. На ее долю выпадает максимальное количество атак, кривотолков и даже нехороших слов. Один из ее противников назвал ее даже «ржавым замком», который запирает ворота на пути дальнейшего движения науки.

Начнем с того, что вернемся к понятию теплорода (у Карно французское слово calorique — «калорик») и представлению о том, как он создает работу (рис. 3.1).

Мы уже говорили о том, что такое понимание связано с теорией о некоем веществе, которое протекает сверху вниз (от высокой температуры к низкой), производя работу; при этом его количество не меняется. С установлением механической теории тепловых явлений это представление, естественно, отпало.

Однако оказалось (как это часто бывает), что в представлении о том, что сквозь двигатель проходит поток «чего-то», не меняющего при его работе свое значение, есть некое рациональное зерно.

Действительно, вникнем немного глубже в уравнение, отражающее принцип Карно, установив из него связь количеств теплоты Q 1и Q 2и температур Т 1и Т 2. Для этого преобразуем его. Очевидно (по закону сохранения энергии — первому закону термодинамики), что Q 2= Q 1— L; тогда основное уравнение Карно можно переписать, заменив работу L на ее значение, так:

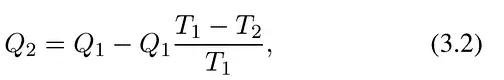
или, после упрощений:

Q 1/T 1= Q 2/T 2(3.3)

Выходит, что отношения количеств теплоты к соответствующим температурам (так сказать, «приведенная» теплота) и на входе теплового потока, и на выходе равны. Значит, действительно, есть тепловая величина, отличающаяся от «просто» теплоты, сохраняющая для двигателя постоянное значение в процессах ее подвода и отвода! [50] Примечательно, что сам С. Карно в определенной степени это чувствовал: везде, где он говорил о теплоте (в смысле величины Q), использовалось слово chaleur (тепло), а где о теплороде — другое, уже упоминавшееся нами слово calorique — теплород. То, что это не случайность, видно из того, что такая терминология ни разу не нарушается.

Замечательное свойство величины Q/T сохраняется и в другом, тоже достаточно важном случае.

Мы уже говорили о том, что двигатель, введенный Карно, — идеальный, т. е. работает без потерь. Это означает, что работа, получаемая от него, максимальна при данных Q 1и температурах Т 1и Т 2, т. е. полностью соответствует величине L в формуле (3.1), Если использовать полученную работу, то цикл может быть пущен и в обратную сторону. Понятие о такой обращенной тепловой машине тоже введено С. Карно в его знаменитой книге. При таком «обращении» идеального цикла все количественные соотношения между величинами, определяющими его работу, останутся прежними, только вместо переноса «теплорода» с высокой температуры на низкую будет происходить обратный процесс — перенос его с низкого уровня температуры на высокий. Для этого потребуется ровно столько же работы, сколько ее было получено, и все вернется в исходное состояние. Другими словами, такой цикл обладает свойством обратимости. На рис. 3.2 показаны оба случая с потоками энергии. Потоки энергии показаны в виде полос, ширина которых пропорциональна потоку энергии. Такие графики называются полосовыми. Отношения Q/T в обоих случаях остаются одинаковыми и на входе теплоты, и на ее выходе.