Виктор Бродянский - Вечный двигатель — прежде и теперь. От утопии — к науке, от науки — к утопии

Закономерность, характерную для идеальных процессов, — существование величины S, которая в сумме не меняется во всех процессах, связанных с переносом энергии, — можно назвать принципом существования и постоянства энтропии.

Если бы свойства энтропии ограничивались только постоянством в идеальных обратимых процессах, то споров вокруг нее было бы значительно меньше. Однако энтропия имеет еще одно важное свойство, именно оно уже более 100 лет вызывает острые споры.

Начало им положил тот же Р. Клаузиус. Он развил идеи С. Карно на новом уровне, основанном на механической теории теплоты, и установил еще одно важное свойство энтропии. Опираясь на него, Клаузиус делает один далеко идущий вывод, из-за которого и возникла дискуссия, продолжавшаяся больше века.

О чем же идет речь?

С. Карно ввел и рассматривал идеальные обратимые процессы, в которых переход теплоты от тела с высокой температурой Т 1— теплоотдатчика — к телу с низкой температурой Т 2— теплоприемнику — сопровождается получением работы; напротив, переход теплоты от теплоотдатчика с низкой температурой Т 2к теплоприемнику с более высокой температурой Т 1происходит с затратой работы. Однако существуют и другие, необратимые процессы переноса теплоты, могущие сами по себе идти только в одну сторону. Именно на них и обратил внимание Клаузиус. Действительно, что будет, если источник теплоты — теплоотдатчик с более высокой температурой Т 1— привести в тепловой контакт (например, соединить металлическим стержнем) с теплоприемником, температура Т 2которого ниже, без тепловой машины? Тогда возникнет тепловой поток от тела с температурой T 1к телу с температурой Т 2; работы при этом, естественно, никакой не производится, и всю теплоту, отдаваемую теплоотдатчиком, получит теплоприемник.

Таким образом, процесс в этом случае будет односторонним, необратимым, поскольку в обратную сторону он идти не может. (Горячая печка может греть холодный чайник, но холодный чайник греть горячую печку не может.) Как будет вести себя здесь энтропия? Теплоотдатчик отдает энтропию S 1= Q 1/T 1; теплоприемник получает энтропию S 1= Q 1/T 2(теплота, получаемая теплоприемником Q 2= Q 1, так как она на работу не расходуется). Поскольку Т 2< T 1, то S 2> S 1. Энтропия возрастает!

Тот же эффект может получиться и при работе тепловой машины, но не идеальной, как у Карно, а реальной, действие которой сопровождается потерями.

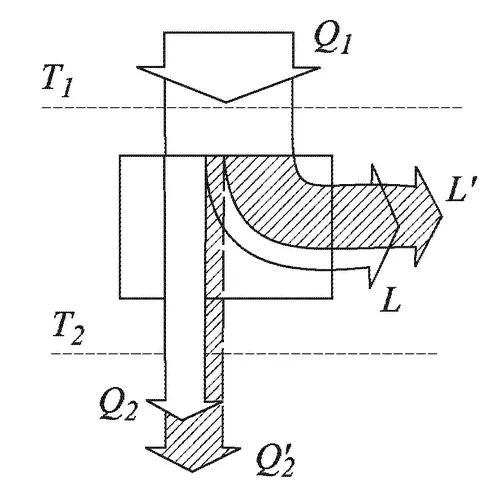
Для реального двигателя это означает, что при тех же температурах T 1и T 2(рис. 3.4) и количестве теплоты Q 1работа будет уже не L, а L' < L. Следовательно, по закону сохранения энергии теплоприемник получит уже большее количество теплоты Q' 2> Q 2, так как в работу ее перешло меньше: Q 2= Q 1— L, Q' 2= Q 1— L'; но L' < L, следовательно, Q' 2> Q 2. Отсюда следует, что полученная теплоприемником энтропия S' 2= Q' 2/T 2> S 2.

Опять энтропия возросла!

Для реального теплового насоса при тех же температурах Т 1и T 2и том же количестве теплоты Q 2затрата работы L' будет больше, чем в идеальном случае: L' > L. Поэтому количество теплоты Q' 1будет также больше, чем Q 1, так как Q' 1= Q 2+ L'. Следовательно, энтропия, получаемая теплоприемником при T 1, будет больше, чем при работе идеального теплового насоса:

S' 1= Q' 1/T 1> S 1– Q 1/T 1.

И здесь энтропия возрастает! Анализ и других реальных необратимых процессов преобразования энергии неукоснительно показывает — энтропия в них, возрастает.

Р. Клаузиус обобщил эту закономерность на любые необратимые энергетические процессы, введя принцип возрастания энтропии: во всех реальных процессах преобразования энергии в изолированных системах [52] Совершенно естественно, что баланс энтропии нужно подсчитывать (как для обратимых, так и необратимых процессов) в изолированных системах. Иначе внешний приток (или отток) теплоты, а следовательно, и энтропии смажет всю картину. суммарная энтропия всех участвующих в них тел возрастает. Это возрастание энтропии при прочих равных условиях тем больше, чем сильнее процесс (или процессы) в рассматриваемой системе отличается от идеальных, обратимых. В тепловом двигателе, например, как мы видели, ухудшение его действия (т. е. уменьшение получаемой из того же количества теплоты Q 1работы L при тех же граничных температурах Т 1и T 2) обязательно сопровождается увеличением энтропии. В тепловом насосе увеличение необходимых затрат работы приводит к тому же результату — росту энтропии. Следовательно, энтропия может выполнять еще одну «должность» — быть характеристикой необратимости процессов, показывать отклонение их от идеальных. Чем больше рост энтропии, тем это отклонение больше.

Таким образом, второй закон термодинамики состоит из констатации двух положений — существования и постоянства энтропии в обратимых процессах (Карно) и возрастания энтропии в необратимых процессах (Клаузиус).

Уменьшение энтропии в изолированных системах второй закон запрещает: оно в принципе невозможно: Примеров таких воображаемых невозможных процессов можно привести много: это самопроизвольный переход теплоты от холодного тела с температурой Т 2к более теплому с температурой Т 1> Т 2, например, закипание чайника с водой, поставленного на лед (или замерзание в жару воды в водопроводной трубе). Нетрудно видеть (рис. 3.5), что энтропия при этом уменьшалась бы, поскольку энтропия S воды в чайнике возрастала бы на Q/T 1, а энтропия S льда уменьшалась на Q/T 2. Двигатель, работающий на «концентрации тепловой энергии, отводимой из окружающего пространства» (т. е. производящий работу или электроэнергию из внутренней энергии равновесной окружающей среды) [53] Такой воображаемый ppm-2 иногда называют монотермическим двигателем, так как он должен работать от одного теплоотдатчика с одной температурой To.c. без теплоприемника с более низкой температурой. Отсюда и монотермический — однотепловой («моно» — один). , относился бы к этой же группе нереализуемых систем. Действительно, получая некоторое количество теплоты Q O.C.от среды при ее температуре T O.C.(а с ней неизбежно и соответствующую энтропию S = Q O.C./T O.C., он выдавал бы некоторую работу, в которой энтропии нет. К чему это привело бы?

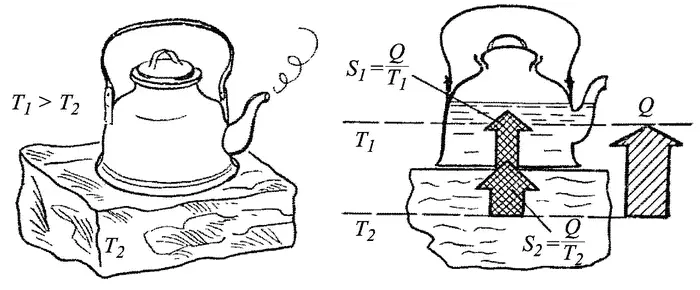
Если бы вся теплота Q O.C.превратилась в работу, то энтропия исчезла бы совсем. Если же в работу L превратилась бы только часть теплоты Q O.C., а остальную ее часть Q 2двигатель отдал бы обратно, то все равно отданная энтропия была бы меньше, чем полученная так как Q 2< Q O.C.и S 2= Q 2/T O.C.< Q O.C./T O.C.