Виктор Бродянский - Вечный двигатель — прежде и теперь. От утопии — к науке, от науки — к утопии

Таким образом, тепловой двигатель превратится в «тепловой насос», перекачивающий «теплород» с низкой температуры на высокую с затратой работы. Поток приведенной теплоты подобно потоку «теплорода» и здесь пройдет неизменным через машину, но не «сверху вниз», как в двигателе, а «снизу вверх», как в насосе. Если бы заснять действие машины на кинопленку, то ее (и машину, и пленку) можно было бы крутить в любом направлении: картина была бы верной во всех случаях.

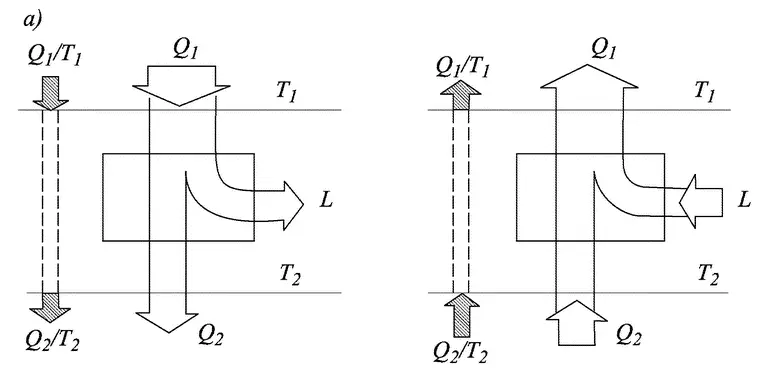
Это замечательное свойство величины Q/T оставаться неизменной при всех идеальных (и, следовательно, обратимых) взаимных превращениях теплоты и работы не могло не обратить на себя внимания.

Р. Клаузиус (1822-1888 гг.) был первым, кто придал величине Q/T самостоятельное значение и ввел ее в науку.

Он назвал ее энтропией. С тех пор (1865 г.) энтропия (ее по стандарту обозначают буквой S) начала свой славный и вместе с тем тернистый путь в науке. Славный потому, что она «работала» и продолжает «работать», помогая решать множество важнейших теоретических и практических проблем (и не только термодинамических). Тернистый потому, что трудно найти другое научное понятие, вокруг которого кипели бы такие страсти и которое вызвало бы столько кривотолков, ошибок и нападок. Достается ей и от идеологов, и от изобретателей ppm-2.

В чем тут дело, станет окончательно ясным, если рассмотреть некоторые свойства энтропии.

Начнем с того, что энтропия имеет еще одно важное свойство, роднящее ее с «теплородом». Она может не только подводиться к телу вместе с теплотой (или отводиться от него), но и, в отличие от теплоты, накапливаться в теле, «содержаться» в нем. При работе двигателя Карно или теплового насоса энтропия, как мы видели, «протекает» через них (рис. 3.2). Сколько ее входит, столько и выходит. Но при нагреве вещества путем подвода к нему теплоты энтропия поступает, но не выходит: она «накапливается» в веществе. Теплота исчезает, превращаясь во внутреннюю энергию, а энтропия увеличивается. Напротив, при отводе теплоты энтропия тела убывает. Таким образом, энтропия может как содержаться в телах, так и посредством теплоты передаваться от одного тела к другому.

Соотношением S = Q/T можно пользоваться тогда, когда все количество теплоты Q отдается при одной и той же температуре Т. На практике температура Т в процессе подвода теплоты большей частью меняется, так как тело нагревается (а при отводе охлаждается). Дня каждой малой порции теплоты δQ температура будет уже другой; поэтому энтропию подсчитывают для каждой порции теплоты отдельно в виде δS = δQ/T и потом суммируют порции энтропии δS. В целом количество энтропии ΔS будет равно сумме малых изменений величины δS; ΔS = ∑δQ/T,, а при переходе к бесконечно малым

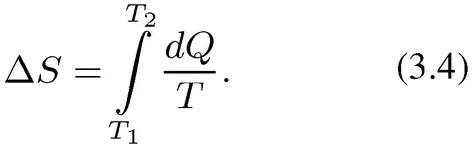
Из соотношения δS = δQ/T следует, что поток теплоты можно представить как произведение температуры T, при которой она передается, на поток энтропии:

δQ = T∙δS (3.5)

Эта формула имеет глубокий физический смысл. Обратим внимание на то, что при передаче энергии в форме механической работы ее количество, как и по формуле (3.5), тоже определяется произведением двух аналогичных величин.

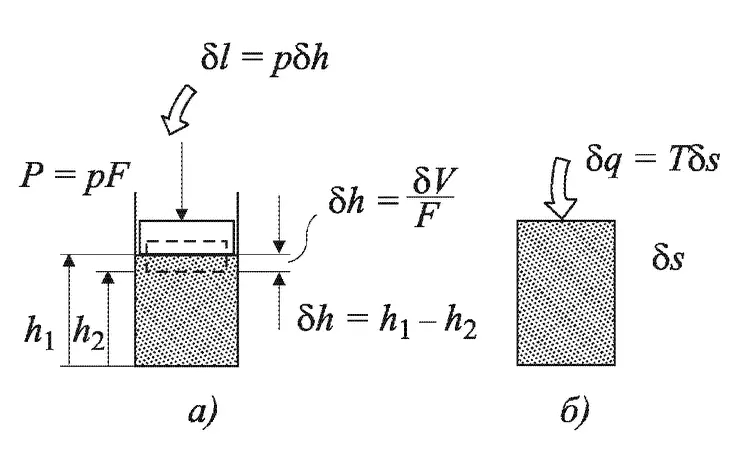
Возьмем два примера — по одному для каждого случая (рис. 3.3): работу сжатия газа в цилиндре (а) и нагрев газа в теплоизолированном сосуде (б). В первом случае работа l равна произведению силы Р (равной произведению давления р на площадь поршня F) на путь δh (равный отношению изменения объема δV к площади поршня F). Так как по мере сжатия газа сила Р должна расти, работу надо считать по малым отрезкам δh, на которых ее можно принимать постоянной. Тогда работа будет составлять произведение двух величин:

δl = p∙δV. (3.6)

Нетрудно видеть, что во втором случае, аналогично первому, для некоторого элементарного количества теплоты δQ, при передаче которого Т неизменна,

δq = T∙δS. (3.7)

Таким образом, передача энергии в двух формах — теплоты и работы (несмотря на их принципиальную разницу — неорганизованную форму в первом случае и организованную во втором) может быть выражена аналогично. Количество энергии в обоих случаях (3.6) и (3.7) выражается произведением двух величин.

Первая из них (давление р для работы и температура Т для теплоты) — это силы (потенциалы), которые вызывают данную форму передачи энергии. Вторая — это «так называемые координаты, изменение которых показывает наличие данной формы передачи энергии. Если координата (V или S) не изменилась (т. е. δV или δS равны нулю), то δL и δQ тоже будут равны нулю и никакой передачи энергии не произойдет.

Первые величины называют еще факторами интенсивности, а вторые — экстенсивности. Следовательно, энтропия — фактор экстенсивности при передаче энергии в форме теплоты. Интенсивные факторы не связаны с массой тела, которому передается энергия, экстенсивные факторы, напротив, зависят от нее: и энтропия S, и объем V при прочих равных условиях тем больше, чем больше масса газа. Соответственно они измеряются в единицах, отнесенных к единице массы.

Понятие об интенсивных и экстенсивных факторах имеет очень широкий смысл, далеко выходящий за пределы термодинамики. Интенсификация любого процесса (даже в народнохозяйственном плане) достигается не за счет увеличения экстенсивного фактора, а только посредством интенсивного фактора. В случае передачи энергии в форме теплоты таким фактором служит температура.

Может возникнуть естественный вопрос: если изменение энтропии, равное нулю, показывает отсутствие передачи энергии в форме теплоты, то как быть с тепловой машиной Карно? Ведь к ней теплота и подводится, и отводится, а энтропия постоянна?

Это противоречие кажущееся: внешние потоки энтропии постоянны, но внутри машины циркулирующее рабочее тело постоянно и нагревается, и охлаждается. При его нагревании двигатель получает теплоту и энтропия рабочего тела растет; при охлаждении и отводе теплоты энтропия уменьшается. В идеальном процессе эти величины равны, и в целом энтропия непрерывно отдается теплоприемнику в том же количестве, что и поступает от источника теплоты. Поэтому круговой процесс — цикл может повторяться сколь угодно долго.