Роджер Пенроуз - Новый ум короля: О компьютерах, мышлении и законах физики

Вопрос об устойчивости (в том смысле, в каком мы трактуем устойчивость здесь) сводится к вопросу о том, остается ли с ростом t область R t локализованной или начинает расплываться по всему фазовому пространству. Если область R t со временем сохраняет конечный объем, то мы будем говорить, что наша система демонстрирует устойчивое поведение. Точки фазового пространства, близкие друг к другу (настолько, что они соответствуют конкретным физическим состояниям системы, которые существенно похожи друг на друга), остаются близкими, и погрешности в указании их положения со временем не увеличиваются. Любое чрезмерно сильное расплывание начальной области R 0 в результате приводит к появлению непредсказуемой составляющей в поведении системы.

А что вообще можно сказать о гамильтоновых системах? Стремятся ли области фазового пространства расплываться со временем или все-таки нет? Казалось бы, при такой общей постановке проблемы сказать о ней можно будет немного. Однако для гамильтоновых систем существует весьма красивая теорема, принадлежащая выдающемуся французскому математику Жозефу Лиувиллю (1809–1882), которая утверждает, что объем любой области фазового пространства должен оставаться постоянным при любых изменениях состояния системы, происходящих в соответствии с уравнениями Гамильтона. (Разумеется, размерность «объема» следует понимать в смысле размерности фазового пространства.) Следовательно, объем каждой области R t должен быть таким же, как объем исходной области R 0 . На первый взгляд теорема Лиувилля позволяет утвердительно ответить на вопрос об устойчивости гамильтоновых систем. В силу того, что размер исходной области (в смысле ее объема в фазовом пространстве) не может возрастать , создается впечатление, будто наша исходная область не может со временем расплываться по всему фазовому пространству.

Однако такое впечатление обманчиво, и, немного поразмыслив над этим, мы поймем, что в действительности может произойти прямо противоположная ситуация! На рис. 5.14 я попытался наглядно изобразить такое поведение системы, которое можно было бы ожидать в общем случае.

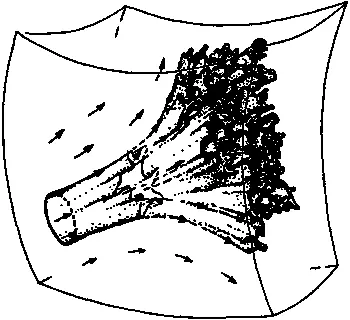
Рис. 5.14.Несмотря на то, что — согласно теореме Лиувилля — объем фазового пространства сохраняется постоянным, он, как правило, будет расплываться в результате чрезвычайно сложной эволюции системы во времени

Представим себе, что начальная область R 0 невелика и имеет «приемлемую» форму — достаточно гладкую, лишенную причудливых выступов — которая указывает на то, что при описании состояний, принадлежащих этой области, чрезмерно высокая точность совсем необязательна. Но с течением времени область R t начинает деформироваться и растягиваться — сначала принимая форму, напоминающую амебу, а затем образуя причудливые отростки, которые простираются далеко в стороны, замысловато извиваясь то в одном, то в другом направлении.

Объем при этом действительно сохраняется, но тот же самый объем может теперь истончиться и распределиться по обширной области фазового пространства. Практически аналогичная картина будет наблюдаться в случае с капелькой чернил, попавшей в большую емкость с водой. В то время, как реальный объем чернильной жидкости остается неизменным, она постепенно истончается, распределяясь по всему объему емкости. Вероятно, подобным образом ведет себя и исходная область R 0 в фазовом пространстве. Она не обязательно должна расплываться по всему фазовому пространству (эта предельная ситуация известна под названием «эргодической») — но вполне может в конце концов занять область, значительно превышающую ее первоначальный объем. (Дальнейшее обсуждение см. в книге: Дэвис [1974].)

Трудность заключается в том, что сохранение объема отнюдь не влечет за собой сохранение формы : малые области имеют тенденцию деформироваться, и их деформации простираются на большие расстояния. В многомерных пространствах проблема расплывания начальной области гораздо более серьезна, чем в пространствах малой размерности, так как «направлений», по которым расплываются отдельные части нашей области, гораздо больше. На самом деле, вместо того, чтобы «помочь» нам держать область R t под контролем, теорема Лиувилля создает фундаментальную проблему! Не будь теоремы Лиувилля, можно было бы представить, что бесспорная тенденция к расплыванию области в фазовом пространстве могла бы (при соответствующих обстоятельствах) компенсироваться уменьшением полного объема. Но теорема Лиувилля говорит нам, что такое уменьшение невозможно , и нам остается только мириться с таким поразительным свойством — универсальным для всех классических динамических (гамильтоновых) систем нормального типа! [113]

Помня о неизбежном расплывании исходной области в фазовом пространстве, уместно спросить: а как в таком случае вообще возможно делать предсказания в классической механике? Это действительно непростой вопрос. Расплывание начальной области говорит нам о том, что независимо от степени точности, с которой мы знаем начальное состояние системы (конечно, в разумных пределах), тенденция к возрастанию погрешностей со временем сделает нашу исходную информацию практически бесполезной. В этом смысле классическая механика в принципе непредсказуема . (Вспомним введенное выше понятие «хаоса».)

Чем же в таком случае объяснить явный успех ньютоновской механики? Говоря о небесной механике (т. е. движении небесных тел под действием сил гравитации), в качестве наиболее вероятной причины можно назвать, наверное, то, что, во-первых, небесная механика занимается изучением сравнительно небольшого числа связанных тел (Солнца, планет и их естественных спутников — лун), между которыми имеется большой разброс по массе, поэтому в первом приближении возмущающим действием менее массивных тел на более массивные можно пренебречь и рассматривать только взаимодействие нескольких массивных тел друг на друга; во-вторых, законы движения, применимые к отдельным частицам, образующим эти тела, как нетрудно видеть, работают и на уровне самих тел, вследствие чего с очень хорошим приближением Солнце, планеты и луны можно, в свою очередь, рассматривать как частицы и не беспокоиться по поводу малых движений отдельных составляющих небесных тел! [114]И снова нам удается свести все к рассмотрению системы из «небольшого» количества тел, где расплывание начальной области в фазовом пространстве становится несущественным.